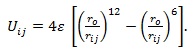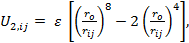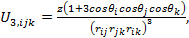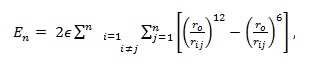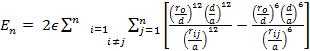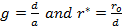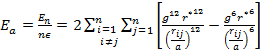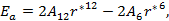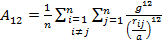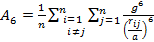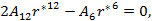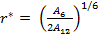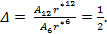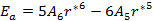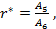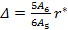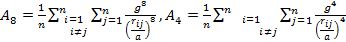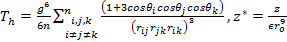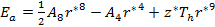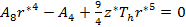International Journal of Theoretical and Applied Nanotechnology (IJTAN)

ISSN: 1929-1248

1. Introduction

Several researchers have tried to simulate the nature of atom-atom interaction, the stability, lattice constant, cohesive energy, and melting phenomena of nanocrystals during the last decade. Models like the surface area difference [SAD] (Qi & Wang, 2002), the extended surface area difference [ESAD] (Qi et al., 2007a), the generalized surface area difference [GSAD] (Qi 2006a), the liquid drop model [LD] (Nanda et al., 2002), the latent heat model [LH] (Jiang et al., 2002a), the bond energy model [BE](Qi et al. 2003), the extended bond energy model [EBE] (Qi et al. 2006b), the generalized bond energy [GBE] (Qi et al. 2007b), the bond-order-length-strength model [BOLS] (Chang et al., 2002 ) were successful to predict the cohesive energy of nanocrystals. The melting temperature and the cohesive energy change linearly. Many researchers (Safai et al.,2007, Qi & Wang 2004a, Qi 2005, Jiang et al., 2000b, Zhang et al., 2000) successfully modelled and predicted the melting temperature of some nano-materials. Other researchers, found quite a distinct structure properties between nanoparticles and nanostructured materials (Y. F. Zhu, et al., 2009). It was noted that some researchers used potential energy functions (PEF) that describe the atom-atom interaction in the bulk material for modelling the atom-atom interactions in the nanocrystals. It must be realized that the interaction within the nanocrystals is totally different from that in bulk material. Whereas, in bulk crystals, the atoms are affected by the electron sea field, they are affected in the nanocrystals by Van Der Waals interactions formed by diploes. The dipoles are formed by the electron clouds along with atoms. This paper develops a test to check whether a PEF correctly describes the interaction within the nanocrystals or not.

There were two main approaches to model the atom-atom interactions in nanocrystals: (i) consider the two, three-body interactions (Qi et al., 2004b, Barakat et al., 2007, Barakat et al., 2009, El-Bayyari 1992a,b, Erkoc 1985, 1988, 1989a,b, 1990, 1992, 1997, 2000 Coles 1990) or (ii) consider the bulk and surface parameters (number of bonds, surface energy, melting entropy, etc.). The size dependence of the thermodynamic quantities of metallic particles was reported as early as 1909 (Jiang et al., 2002a).

Non-bonded interactions can be divided into two classes: short and long range interactions. The short range repulsive forces result from the overlapping of electron cloud. The models investigated in this paper comprise at least two inverse power terms. The ratios of the powers range between "1" and "2". One of the terms is attractive (negative potential energy) and the other is repulsive (positive potential energy). The attractive term is considered to be "long range" while the repulsive term is "short range". The attractive term has been found to have less exponent power than the repulsive (Kittel 1995). Long range and short range terms have always been an interest for scientists involved in research related to molecular dynamics, molecular interactions, condensed matter, and nano-science.

In this paper models and methods of the calculation are explained in section 2. Following that the discussion of the findings and results are given in section 3 and concluding remarks are given in section 4.

2. Model and Method of Calculations

The method adopted in this study is based on the size dependent potential parameters (SDPP) method. The metallic nanocrystals are generated from ideal FCC and BCC crystal structures assuming a similar internal structure of the bulk. The method of counting particles in a given size is simple. One of the atoms is taken as the central one and the radii of the shells are integer multiples of the lattice parameter 'a'. The determination of the number of shells, the radius, the position of individual atoms and the total number of atoms in the nanocrystal can also easily be found.

The three different models proposed by three research groups which successfully describe the size dependence of the cohesive energy of nanocrystals follow:

(i) Lennard-Jones model where atoms are assumed to interact via the potential: (Deltour et al. 1997)

(1)

(ii) Mie-type model with the atom-atom interaction described via the potential: (Aydogdu & Sever, 2010)

(2)

where r_ij denotes the distance between atoms i and j, r_o denotes the equilibrium separation between the centers of any two atoms, ε denotes the pair energy at r_o, m, and k are adjustable parameters.

(iii) A Mie-type combined with Axilrod-Teller three body term as: (Axilrod & Teller, 1943)

(3)

(4)

where θ_i, θ_j, θ_k and r_ij, r_jk, r_ik represents the angles and the sides of the triangle formed by the three atoms, i, j, and k respectively. The parameter z is the intensity of the three body interaction.

The internal energy is given by the sum of the potential and the kinetic energies. At 0 K the total energy is given by the potential energy. It was found that the difference between the cohesive energies of bulk metals at 0 K and their melting temperatures are less than 5% (Kittel 1995). So, in this study, the calculations are conducted at 0 K and the total energy can be found by summing the potential over all the atoms in the nanocrystal as (for model (i)):

(5)

which can be written as;

(6)

(7&8)

equation (6) reads

(9)

'g' has definite values for each structure. It has the values of (√3)/2 for BCC and 1/(√2) for FCC structures. r_ij/a is the same for all elements of the same structure, so eq. (9) will describe fairly well the behaviour of all elements of a certain structure. The binding energy per atom of a spherical metallic nanocrystal with cubic structure is:

(10)

(11)

where

(12)

(13)

The stability condition for cubic crystals 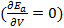at T=0 K is imposed to obtain the minimum energy configuration. 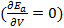which is equivalent to 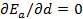since V and d are related via the relation 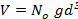, where 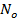is Avogadro's number. That means

and

(14)

the ratio of short range to long range terms is given by:

(15)

(16)

(17)

for which the ratio Δ is given by

(18)

The results in eqs. (15) and (18) can be generalized for two-body Mie-type potential to have:

(19)

The total energy for the last model to be discussed in this paper is given by:

which can be written as:

(21)

with g and r* defined as in eqs. (7) and (8).

(22)

(23)

Equation (21) can be written as

(24)

The stability equations reveal:

(25)

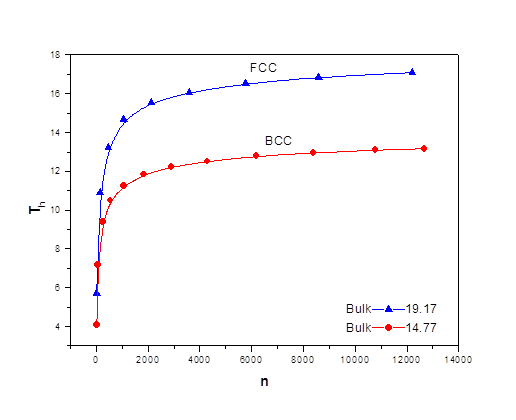
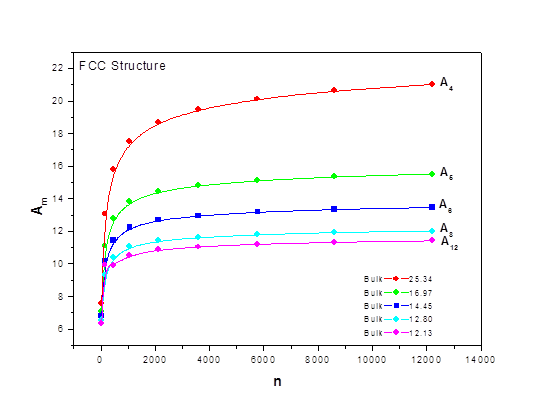
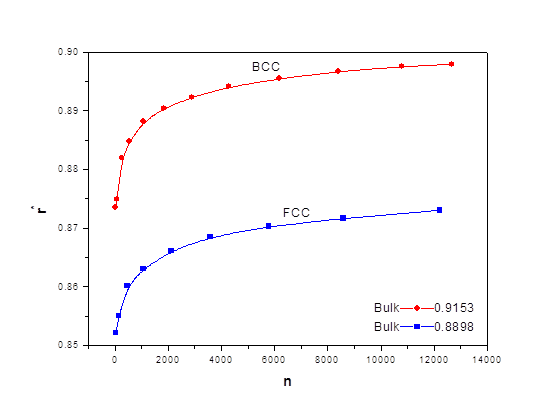
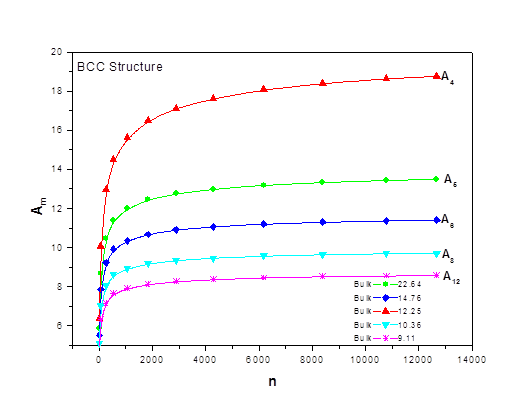
As the size of nanocrystal changes, the ratio r* changes. The values of A₄, A₅, A₆, A₈, A₁₂, and T_h for FCC and BCC structures are given as a function of the number of atoms 'n' in the crystal in figures 1, 2, and 3 respectively. From these figures, it is apprehensible that the parameters A_i and T_h depend on the structure of the nanocrystal. In addition, A_i depends on the exponent of r_ij/a. As the exponent approaches ∞, Ais approaches the number of nearest neighbours of a certain structure. The ratio r_ij/a represents the locations of the lattice points in space for the respective structure. Therefore, the summation can be easily found by summing over all lattice points within the spherical shell of the nanocrystal. z* is the intensity of the three-body term in the potential and can be found where FCC and BCC have a common minimum energy. The value was found by T, Barakat et al. (Barakat et. Al 2009) to be 0.72. As such r* can be found from equation (25) and its value depends on the nanocrystal size and structure as shown in figure 4.

For this model, the three-body term acts either as a short range, a long range or as a mixture of both (medium range). In general it ranges between 24-30% of the long range two-body term, so it does not affect the behaviour of Δ in general, since it changes very slowly.

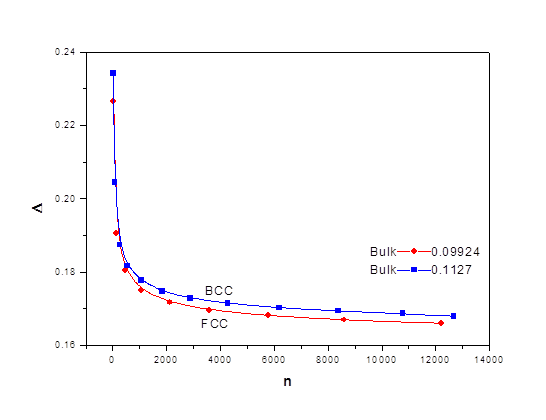
The ratio Δ as a function of n is shown in figure 5, where it shows size dependence for BCC and FCC, respectively. The long range term is dominant and the short range forms 23% to 17% of the long range for both FCC and BCC structures.

The stability equations reveal:

(25)

The ratio Δ as a function of n is shown in figure 5, where it shows size dependence for BCC and FCC, respectively. The long range term is dominant and the short range forms 23% to 17% of the long range for both FCC and BCC structures.

3. Discussion

The two models proposed by W. Qi et al. (Qi W. H. et al. 2004b) and T. Barakat et al. (Barakat T. et al. 2009) which include the Lennard-Jones (12,6) and Mie-type (6,5) respectively, reveal a constant ratio between the long and short range terms of the potential. For Lennard-Jones potential the long range term is twice that of the short range regardless of the structure and the size. For the Mie-Type (6,5), Δ approaches unity, as if the short range and long range are equal. The effects of long range and short range overlap.

Figures 1, 2, and 3 show the size dependence of the lattice sums for FCC and BCC structures. It can be seen from these figures that these parameters increase rapidly as the size of the nanocrystal increases and converge to their bulk values as n reaches 2000 atoms.

The ratio r* represents the instantaneous dual change of ro and d. It is given by r_o/d or equivalently by r_o/ag, where "a" is the lattice constant. Figure 4 show its size dependence as well as its quick convergence towards the bulk values for both FCC and BCC. This figure shows that r* increases as the size increases. This means that the lattice constant "a" decreases as the size increases. It is quite interesting and unclear that "a" decreases as the size increases for nanoparticles, while the reverse is predicted for nanostructured materials.

The ratio of the short to the long range terms is shown in figure 5 for both FCC and BCC respectively. Δ approaches 10% at the bulk. The short range term is crucial for small nanocrystals where it forms 23% of the long range term. It decreases rapidly and starts saturating at n greater than 2000 atoms.

4. Conclusion

Three models for the potential energy function have been used to investigate the test proposed in this paper. The first was the two-body Lennard-Jones, the second was the Mie-type with (m, k) as (6, 5) and the third is composed of a Mie-type with (m, k) as (8, 4) combined with Axilrod-Teller triple dipole terms. Different parameters and lattice sums of all the three PEF's were calculated where they showed size dependence and the correct convergence toward their bulk values. Models (i) and (ii) revealed a constant ratio of the short- to the long-range terms of the PEFs as 0.5 and 0.83 respectively. These results contradict the acceptable behaviour of the short and long range terms as one expects an increase in short range term when the atoms get closer and vice versa.

Model (iii) predicted to a high accuracy the experimental data for Mo and W. According to present work based on this model, the ratio of the short- to the long-range terms of the PEFs initially decreases rapidly with increasing the number of atoms in the nanocrystal reaching 170% of its bulk value at n = 2000 atoms. On increasing the number of atoms, the Δ exhibits a gradual decrease till the number of atoms in the nanocrystal exceeds 12000 for both FCC and BCC structures. The three-body part was fine tuned by the parameter z* to give a stability condition at z* = 0.72 for both FCC and BCC structures. In conclusion, this work demonstrates the dependence of both the short- and long-range terms of the potential energy function of metallic nanocrystals on the range of the potential as well as the size and structure.

Model (iii) also in specific, describes correctly the behaviour of the ratio at the extremes values( i.e. n approaches to 0 and bulk) where the long range term gets smaller and larger respectively.

References