International Journal of Theoretical and Applied Nanotechnology (IJTAN)

ISSN: 1929-1248

1. Introduction

Cellulose nanofiber (CNF) is a fairly new nanomaterial made from various resources of cellulose. It has recently attracted much attention in many fields [1], such as electronic devices, medical material, and food additives. One of the significant features is its high aspect ratio; a typical width is 4-100 nm while the length is often more than 5 μm. It is so light and tough that many applications as structural material are proposed, such as automobile bodies. Cellulose is a renewable resource since it is mainly made from wood pulp.

To fabricate CNF from conventional cellulose resources (e.g., wood pulp and grass), some treatment is required to smash macromolecules of cellulose. Currently exist two major fabrication methods: (i) Chemical treatment [2][3], which uses hydrolysis reactions with strong acid or catalysts. This is not environment-friendly nor cost-effective. (ii) Mechanical approach [4], in which the pulp is mechanically smashed or ground under high shear force. It generally gives fiber size larger than 15 nm. Less popular treatment is hydrolysis using supercritical water [5], which is environment-friendly and has a possibility of precise size control, but its detailed mechanism is not fully understood.

In this study, we focus on the cellulose hydrolysis in supercritical water. To analyze the chemical reaction in atomic scale, we executed a series of molecular dynamics (MD) simulations with quantum effects taken into account as the density functional tight binding (DFTB) model.

2. Methods

In the density functional (DF) theory, the wave function of single electron  and the eigen value (orbital energy) is obtained self-consistently from the Kohn-Sham equation,

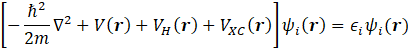
where V(r) is the potential defining the interaction between an electron and the collection of atomic nuclei, V_H(r) the potential for the Coulomb repulsion between the electron and the total electron density, and V_XC(r) the potential for everything else.

In addition, we utilize the tight binding (TB) model in which every single-electron wave function is expressed as a linear combination of atomic orbitals,

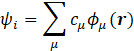
where ϕ_μ(r) is the atomic orbital.

We have utilized the DFTB+ software [6] to perform the ab initio calculation. A self-consistent charge (SCC) DFTB calculation is executed with the third order correction [7]. The 3ob-3-1 parameter set [8] is adopted, which is known to be well applicable to a wide range of organic and bio molecules. Use of appropriate hydrogen bond correction is relevant to our investigation, and we adopted a damping method for modification of short-range potential energy U [7], as

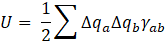
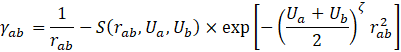
where r_ab is the distance between atom a and b, Δq_i the electric charge on atom i, U_i the Hubbard parameter of atom i, and S a short-ranged damping function [7].

Assuming the Born-Oppenheimer approximation, the equation of motion for each atom is integrated using the velocity Verlet dynamics with the Nosé-Hoover chain thermostat [9] algorithm. We used the 1 × 1 × 1 Monkhorst-Pack grid [10] for k-point sampling (the Γ point calculation).

3. Evaluation of critical point

Before starting the main simulations of hydrolysis, the critical point of the model water should be determined. Using 100 water molecules confined in a cubic simulation cell of various sizes with periodic boundary conditions, we performed the DFTB-MD simulations under constant temperature conditions. Three temperature conditions were investigated, 400, 650 and 800 K. The time step was chosen to be 0.5 fs. Typical snapshots are shown in Figure. 1.

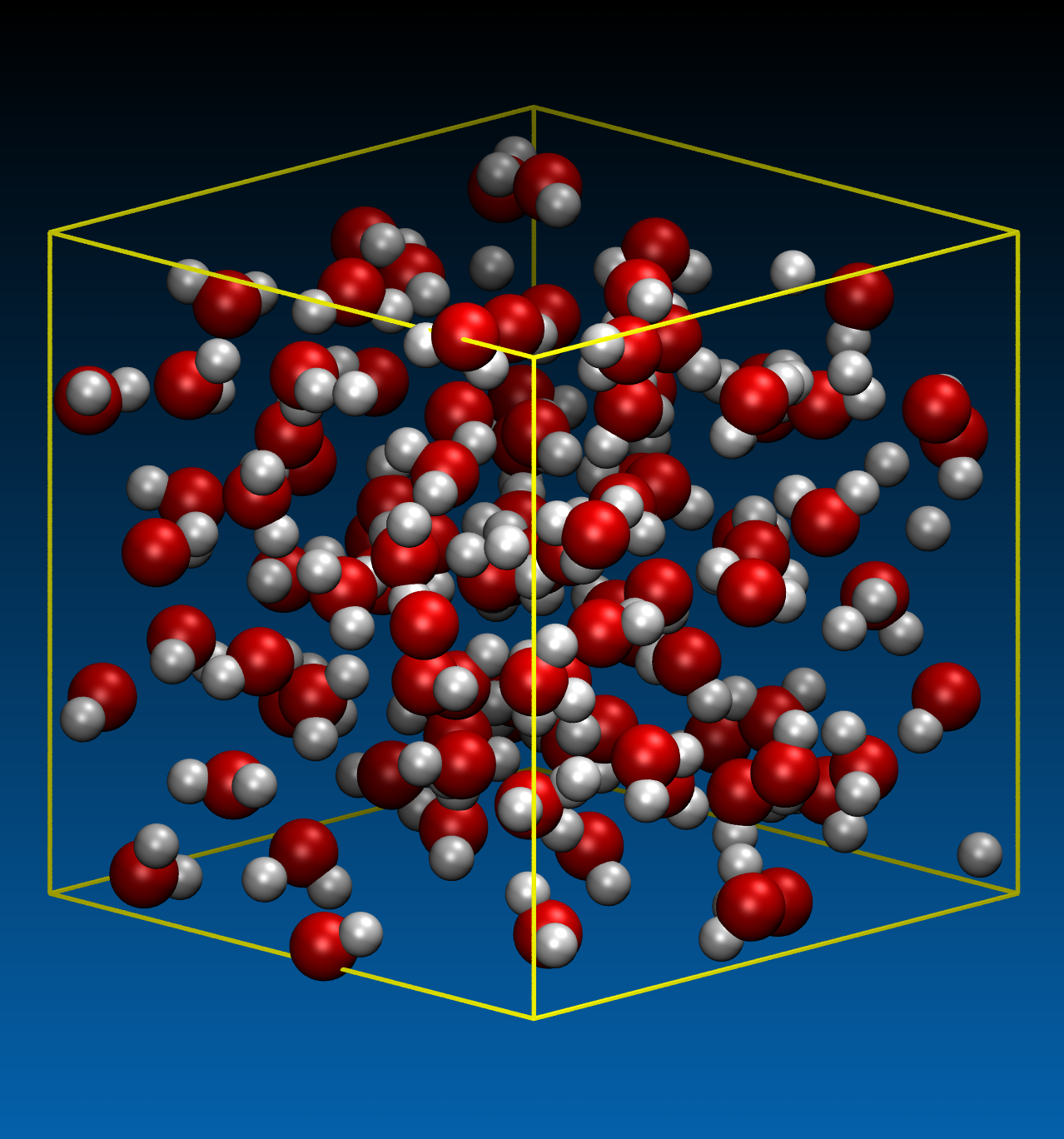
(a) T= 650 K, ρ = 0.886 g/cm³ (cell size: 15 ×15 × 15 A³)


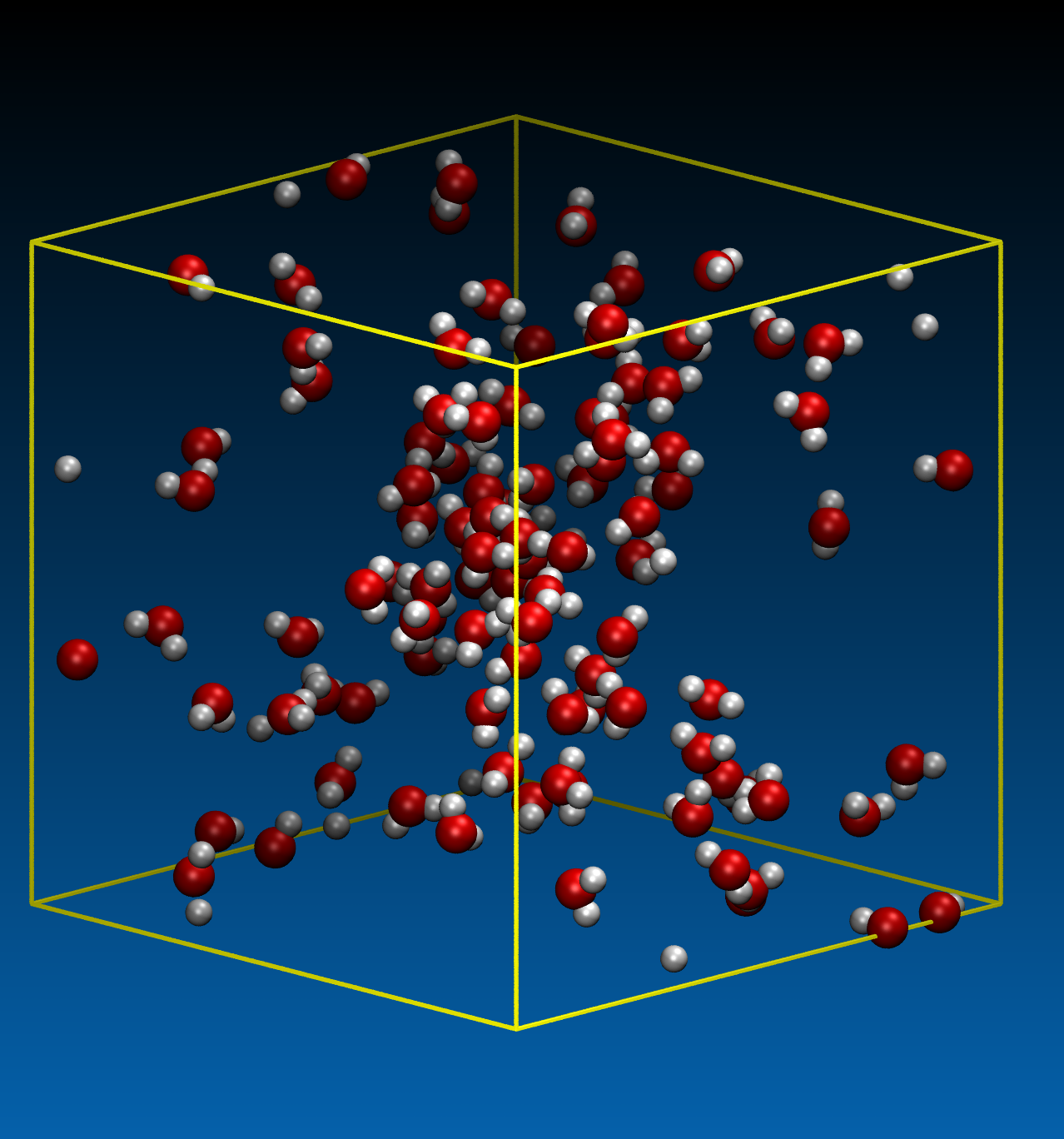
(b) T= 650 K, ρ= 0.191 g/cm³ (cell size: 25 ×25 × 25 A³)

After equilibrating the system, the mean pressure was evaluated. The obtained P- V curve is shown in Figure. 2, which suggests that the liquid-vapor critical point of this model water exists around (T_c,V_c ,P_c ) = (650 K , 80 A³, 21.9 MPa); 80 A³ per molecule corresponds to the density ρ ∼ 0.374 g/cm³. A reported experimental value is (647 K, 0.322 g/cm³, 22.1 MPa) [11], and the agreement is reasonable.

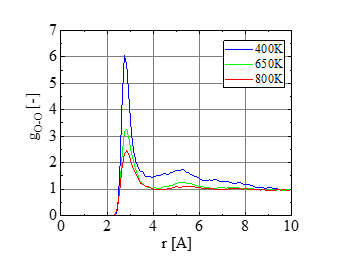
To look at the fluid structure near the critical point, the oxygen-oxygen radial distribution function  is calculated at V= 80 A³. Based on the results shown in Figure. 3, coexisting of liquid and vapor states is suggested at 400 K, while uniform gas phase is realized at T = 800 K. A snapshot at T = 400 K (Figure. 4a) indicates the formation of a huge cluster. On the other hand, water molecules spread homogeneously at T = 800 K (Figure. 4b). Thus we suppose that the state in between (650 K) is close to the critical point. Based on these results, we performed the main simulation of hydrolysis at T≥ 650 K.

(a) T = 400 K.


(b) T = 800 K.

4. Hydrolysis Simulation of Cellulose

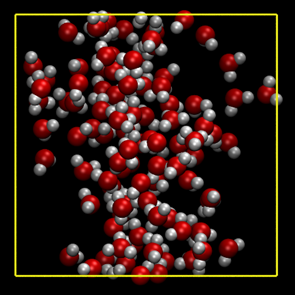
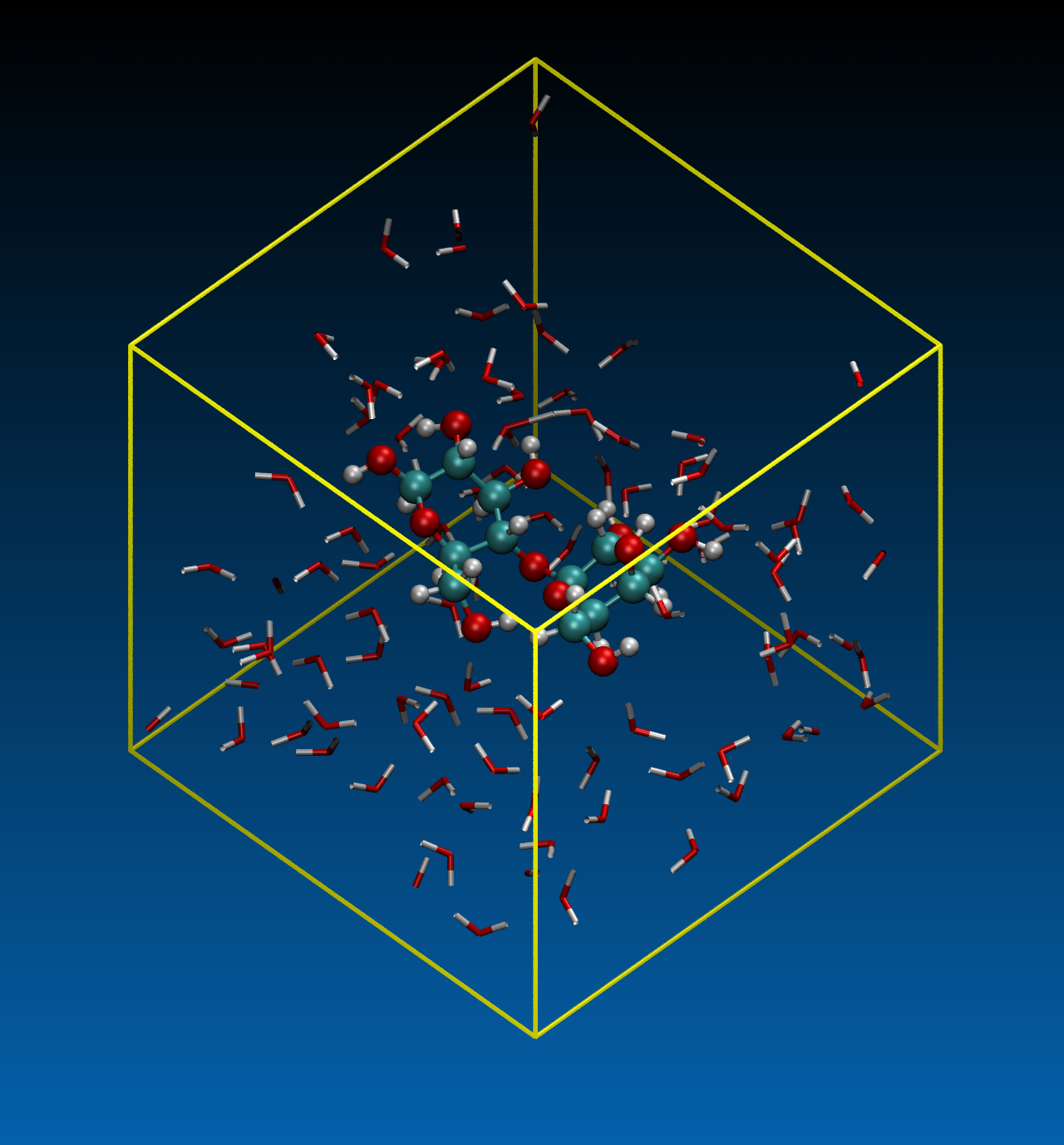
We performed DFTB-MD simulations for the hydrolysis cellulose in water at supercritical states. To reduce the computational resource, a minimum unit of cellulose, i.e., cellobiose (Figure. 5), was targeted. We investigated a system of a single cellobiose molecule surrounded by 100 water molecules (Figure. 6). The cell size was 17.197 × 17.197 × 17.197 A³ (0.70 g/cm³) and the periodic boundary conditions were assumed for all directions. Constant temperature MD simulations were carried out at four temperatures, T = 400, 650, 800 and 1000 K. A shorter time step of 0.25 fs was used to see the trajectories more precisely.

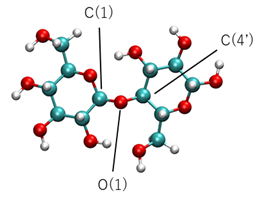
For the hydrolysis of large cellulose molecules, cleavage of the 1,4-β-glycosidic bond, shown in Figure. 5, is essential. Since this is a stochastic process, we counted the number of cleavage cases out of ten trials with different initial configurations; each trial run is 12.5 ps (50,000 steps). The results are summarized in Table 1, which indicates that the hydrolysis of cellobiose is more probable near the critical point of fluid water.

Table 1. Summary of simulation results. Each trial is a 12.5 ps MD simulation.

Temperature [K]	Trial	Bond cleavage
400	10	0
650	10	2
800	10	3
1000	10	1

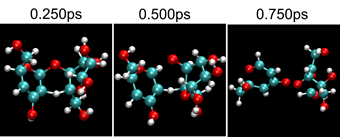
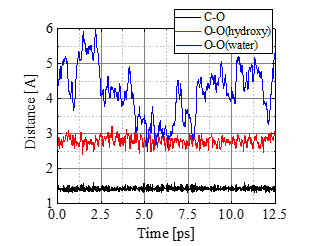
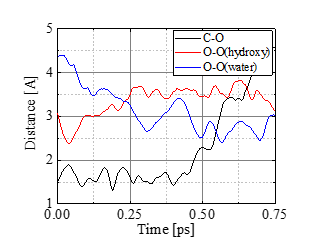
Figure 7 shows a series of snapshots of the bond cleavage at T = 1000 K. After t = 0.25 ps, the bond breaks while a weak carbon-carbon bridge via a hydrogen atom is newly formed, temporarily maintaining the dimer. In Figure.8 comparison is made between T = 400 and 1000 K cases for the atomic distances; the glycosidic bond between C and O atoms is indicated with black lines, while the distance between the glycosidic O and the nearest hydroxyl O is shown with red, and the glycosidic O and the nearest water O with blue. At 400 K, water molecules cannot get close to C because the adjacent hydroxyl group blocks it. Under higher temperature such as 1000 K, some of the water molecules have high kinetic energy (large translational momentum) and are enabled to approach the bond, as seen in Figure.8b, leading to the bond breakup.

(a) T = 400 K.


(b) T = 1000 K.

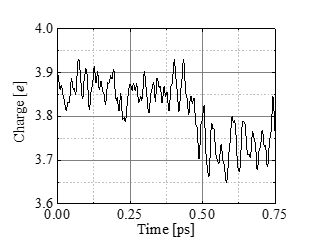
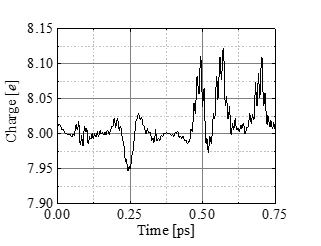
Figures 9 and 10 show the change in the number of electrons (Mulliken charge) assigned to the C(4’) atom and the nearest neighbor water molecule to the bond. Figure 9 indicates that the Mulliken charge decreases during the bond cleavage. This decrease of electrons is roughly compensated by the increase for the nearest water molecule (Figure.10). Thus we conclude that the water molecule approaching the bond with high kinetic energy deprives the C(4’) partially of electrons and initiates the bond breakup.

4. Conclusion

We examined a model cellulose in fluid water with quantum molecular dynamics simulations to study the mechanism of hydrolysis under supercritical conditions. In the normal states, the 1,4-β-glycosidic bond is protected by hydroxyl groups from surrounding water molecules. Under high temperature conditions, the number of water molecules with larger kinetic energy increases so that some of them can approach the glycosidic bonds of cellulose molecules. The water molecule close to the bond attracts an electron from the carbon atom, leading to the bond breakup.

References