International Journal of Theoretical and Applied Nanotechnology (IJTAN)

ISSN: 1929-1248

Nomenclature

• A: vector potential
• A: channel cross sectional area
• B: flux density
• B: blood compartment
• b: concentration of microspheres
• b_500nm: concentration of 500 nm microspheres
• c_e: empirical constant
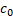• : concentration of bound bacteria
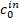• : initial concentration of bacteria
• E: device compartment
• F_drag: drag force
• F_mag: magnetophoretic force
• f: fraction of bacteria removed
• G_i: bacterial growth rate
• H: magnetic field
• H: liver compartment
• H_c: magnetic coercivity
• h: channel height
• J: current density
• k_B: Boltzmann’s constant
• k_d: collision rate constant, diffusion
• k_shear: collision rate constant, shear
• L: lung compartment
• l: channel length
• m: magnetic separation efficiency
• N_b: number of microspheres per bacterium
• n: number of channels
• p_i: partition coefficient
• Q_E: device volumetric flow rate
• Q_i: compartment blood flow rate
• r_c: cell radius
• r_n: cell-nanoparticle conjugate radius
• S: spleen compartment
• T: temperature
• t_inc: incubation time
• t_res: residence time in channel
• V_i: blood volume
• w: channel width
• x: binding efficiency
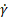• : shear rate
• µ: magnetic permeability
• µ_o: vacuum magnetic permeability
• µ_r: relative magnetic permeability
• η: viscosity
• ρ: fraction of cell surface covered by microspheres
• ν_mag: magnetophoretic velocity
• χ_ν: volumetric susceptibility

1. Introduction

Bacteremia is defined as the presence of bacteria in the blood, usually from an infection source within a tissue. The systemic immune response syndrome (SIRS) resultant from the bacteria and their endotoxins can progress to life-threatening organ dysfunction, which is known as sepsis [1]–[3]. If not properly addressed, sepsis can quickly advance to include more serious complications, with mortality estimated between 28 and 50 percent [4], [5]. Even after treatment, patients can suffer from sepsis recidivism, recurrent or persistent organ dysfunction, or cognitive and functional impairment [6], [7].

In most developed countries, the incidence of sepsis is estimated to be between 50 and 100 cases per 100,000 people; this incidence is increasing in excess of population growth [5]. Immunocompromised patients –­ for example, the elderly, neonates, and hospitalized patients – are especially susceptible to bacterial infections. Approximately half of severe sepsis cases occur in patients already in intensive care [8], and these infections are eight times as likely to result in death when compared with other diagnoses [9]. In total, sepsis results in additional annual healthcare costs of more than $17 billion [4].

Given the complexity of the host-pathogen interactions and the number of infectious pathogens, there is no “gold standard” diagnostic or treatment for sepsis. After suspicion of a bacterial infection, broad-spectrum antibiotics are administered, followed by a more specific antibiotic after confirmation of the pathogen. Unfortunately, with each hour effective antibiotic therapy is delayed, survival decreases by 7.6% [10]. Achieving efficacious treatments becomes more difficult as an increasing number of pathogenic bacteria develop resistances to broad spectrum antibiotics, prompting major health organizations to classify combatting antimicrobial resistance as high priority [11], [12].

Effective treatment of bacteremia involves elimination of bacteria at the source of infection. However, migration of bacteria from an initial infection site to other tissues makes treatment increasingly difficult.  The lungs, liver, and spleen are tissues of particular interest, since they suffer some of the greatest burdens in bacteremia cases [13]–[17]. The removal of bacteria from the various infected organs can be modeled as a clearance mechanism, lending credence to a multi-compartmental physiologically-based pharmacokinetic (PBPK) model. Several PBPK models of bacterial infection have been developed, one of the first being Cheewatrakoolpong et al.’s two-compartmental murine model [18]. Miller et al. were the first to incorporate an extracorporeal pathogen removal device into an infection model [14]. A magnetic separation model was developed by Kang et al. for their device, interrogating the role of the radius of their magnetic beads in separation efficiency from whole blood [19]. Combining these models allows for better understanding of the pharmacokinetics of extracorporeal pathogen removal via magnetic beads and can inform the selection of bead radius, incubation times, and device flow rates.

Understanding the magnetic field is necessary to calculate the motion and separation of paramagnetic particles. Specifically, the force on paramagnetic particles is directly proportional to the magnetic flux density gradient. The partial differential equations (PDEs) that describe the magnetic field and magnetic flux density cannot be solved analytically if complex geometries are involved, such as multiple magnets. The field of the magnets to be used in the separation device were explored in various configurations to optimize the separation of paramagnetic particles.

2. Methods

2.1. Magnetic Field Modeling

The program FEMM 4.2 was used to calculate the magnetic field, , and flux density, , of the magnets. The general time-invariant magnetostatic problem has the governing vector equations.

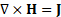
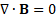
where  is the current density. The constitutive equation

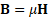
which relates the field to the flux density by the permeability, , must be used for each linear material in the domain. FEMM solves these equations using a magnetic vector potential approach, defining the magnetic flux density in terms of a vector potential, ,

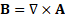
This allows the magnetic field governing equation to be rewritten as

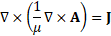
at which point  can be solved for using finite element analysis (FEA).  and  can then be derived from .

Two rectangular neodymium (NdFeB) magnets (K&J Magnetics, BX04X0, Grade N42 NdFeB, 1" x 1/4" x 1" thick, relative permeability , coercivity ) were simulated and separated by 25mm in an attracting configuration to accommodate the microfluidic channels. The poles of these magnets are located on the thinner sides rather than on the square faces, making them ideal for a low-profile separator. The flux density field across the gap in the y-direction was computed and then differentiated in Matlab 2016a to determine the magnetic flux density gradient, .

2.2. Magnetic Separation Model

The binding efficiency of particles to A. baumannii was estimated. As discussed by Kang et al. [19], the concentration of bound bacteria, , as a function of microsphere radius and incubation time is given by

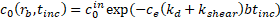
where  is the initial concentration of bacteria;  is an empirical constant to account for changes in binding efficiency in biologically relevant fluids;  and  are the collision rate constants of diffusion and shear, given respectively by

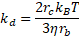
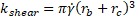
with Boltzmann’s constant, ; the ambient temperature, ; the viscosity of blood, ; the spherical radius of the cell, ; the empirically determined shear rate, ; and  as the incubation time.  The concentration of microspheres, , is calculated relative to a given concentration of 500 nm microspheres, , by the relation

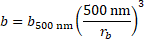
The overall binding efficiency, , is therefore calculated as

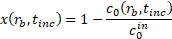
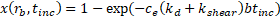
After incubation, the microspheres and microsphere-bacteria complexes are separated out via the magnetophoretic force ,

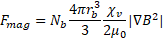
with the constants , the vacuum magnetic permeability;, the volumetric susceptibility of the microspheres; and , the magnetic flux density gradient.  is the number of microspheres bound to a bacterium and is estimated by

Here,  refers to the proportion of the cell surface covered by microspheres.

Opposing the magnetophoretic force is the drag force, , in terms of the magnetophoretic velocity, , given by Stokes flow

where  is the effective hydraulic radius of a microsphere-bacterium complex given by

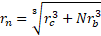
Solving  for  under the assumption of force equilibrium, the magnetophoretic velocity of the complexes is equal to

Therefore, the magnetic separation time across a channel with width  can be calculated as

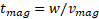
Assuming steady flow in the separation channels, the average velocity of a complex, , is given by

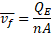
 being the volumetric flow rate through the entire device,  being the number of channels, and being the rectangular cross-sectional area of a channel with height  and width . The residence time in the channel,  , with length  can be calculated as

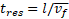
The magnetic separation efficiency, , is then estimated by

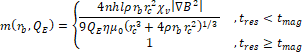
After the incubation and separation stages, the overall fraction of bacteria removed, , can be expressed as

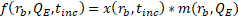
Table 1 lists the physical constants and parameters used for all of the simulations. The device-specific parameters (width, height, length, and number of channels) are based on a microfluidic design currently in use.

Parameter	Value and units	Parameter	Value and units
	107 CFU/mL		3.5
	3.7 x 10-4		0.5
	300 K		1 x 10-4 m
	4.0 x 10-3 kg m-1 s-1		2
	0.5 x 10-6 m		5 x 10-5 m
	1.0186 s-1		2.5 x 10-2 m
	0.0025 kg m-3

 

2.2. Physiologically-Based Pharmacokinetic Model

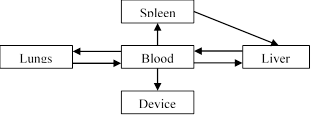
The fractional magnetic separation from Equation 20 factors into the five-compartment PBPK model of infection diagrammed in Figure 1 and detailed in Equations 23-27. Each physiologic compartment has its own associated growth rate, , blood volume, , blood flow rate, , and partition coefficient to bacteria,  (Table 2). The arrows in Figure 1 represent the transport of bacteria between compartments. The blood of the systemic circulation flows to and from each of the organs, except notably where blood is transported from the spleen to the liver via the portal vein. Additionally, the most significant modification from the model published by Miller et al. [14] is the removal of the return pathway from the device to the blood. Here, it is assumed that any bacteria captured have no path of reentry into the circulatory system; consequently, uncaptured bacteria remain in the blood compartment.

 

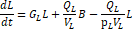
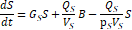
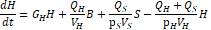
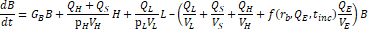
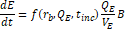
Six different infection and treatment scenarios were then simulated using the coupled differential equations. First, a non-immunocompromised human, an immunocompromised (neutropenic) human, and an immunocompromised human with antibiotic administration were simulated. These three scenarios were then simulated again with the extracorporeal device. A simulated bolus of 10⁷ CFU/mL of A. baumannii was injected into the lung compartment and allowed to proliferate in the system for ten hours. After incubating the blood with the colistinated magnetic microspheres for  5 min, the extracorporeal device was linked into the system and was run for 96 hours. Matlab 2016a’s 4^th-order Runge-Kutta differential equation solver was used to calculate an approximate solution to the system of differential equations. To determine the efficacy of treatment, the area under the curve (AUC) in each of the compartments, computed via trapezoidal integration, was compared across flow rates and microsphere radii. As a quantifiable criterion, the time to go below a threshold of 1 CFU/mL in the bloodstream was also examined [14].

Table 2. Parameters for PBPK model of A. baumannii infection by compartment as given by Miller et al. [14]. N = normal, IC = immunocompromised, AB = antibiotic + IC. Flow rate measured in m³ h^-1, volume measured in m³, growth rate is measured in h^-1, and the partition coefficient is dimensionless.  is varied.

			N	IC	N	IC	AB
L	0.090	4.50 x 10-4	93	3	-1.74	0.21	-0.24
S	0.015	2.09 x 10-4	59	28	-0.14	0.14	-0.07
H	0.048	1.56 x 10-3	749	79	-0.10	0.10	-0.18
B	N/A	N/A	N/A	N/A	-0.17	0.08	-0.05
E		2.5 x 10-10	1	1	N/A	N/A	N/A

3. Results and Discussion

>

3.1. Magnetic Field Modeling

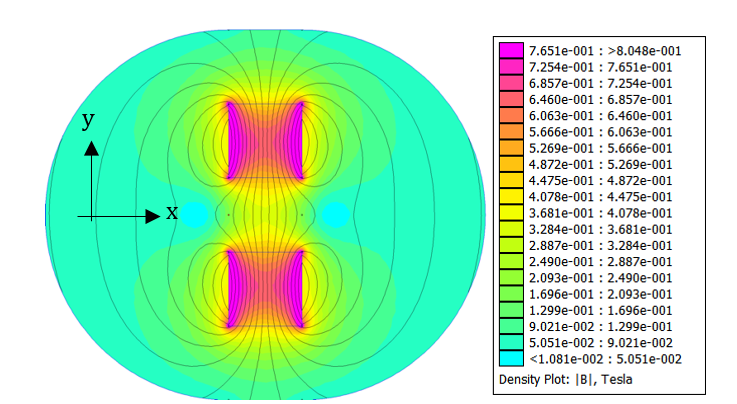
The domain around two rectangular NdFeB magnets was simulated via FEA with 4574 nodes and 8721 elements. The calculated two-dimensional magnetic flux density is consistent with the manufacturer’s documentation for a single magnet (Figure 2) [20]. Maximum flux density occurs inside the magnets along the edges parallel to the poles, while the magnetic field lines towards the boundary of the simulation loop from the north pole of one magnet to the south pole of the other. Similarly, the magnetic field lines connect the closest poles of the two magnets and approach being parallel.

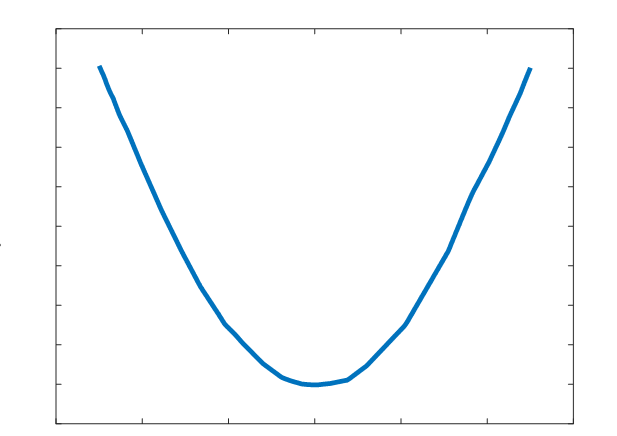
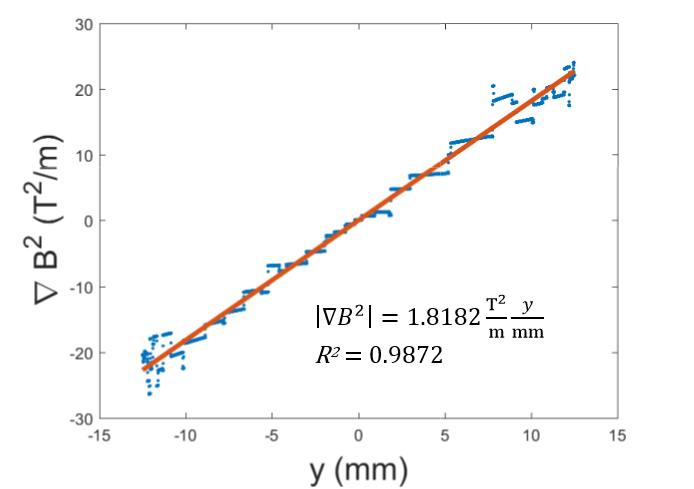
A parabolic profile with a maximum flux density of 0.521T and a minimum field strength of 0.360T was achieved across the channel (Figure 3). Differentiating this with respect to position, the magnetic flux density gradient is approximately linear and ranges from approximately -20 T²/m to 20 T²/m (Figure 4). At the location of the microfluidic channels, 2.1mm from the center of the space between the magnets, the magnetic flux density gradient was estimated to be 4.7 T²/m. With this magnetic flux field, a linear magnetic flux density gradient can be established to ensure consistent separation of magnetic complexes. Furthermore, the magnetic flux density gradient can be tuned to increase separation efficiency.

3.2. Physiologically-Based Pharmacokinetic Model with Magnetic Separation

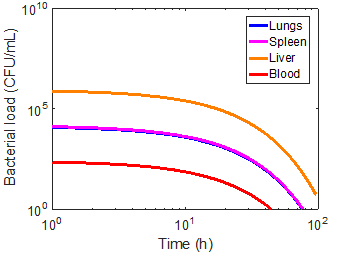
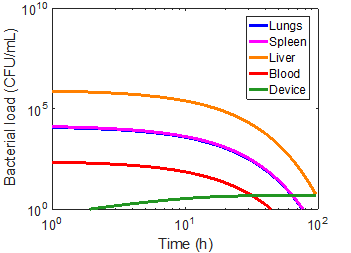
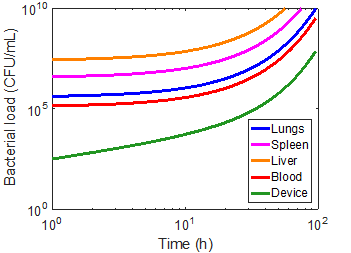
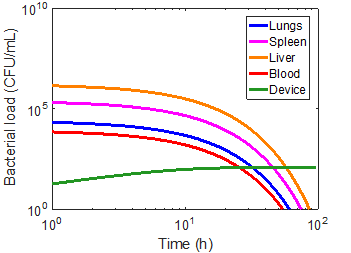
Using the magnetic flux density gradient from the magnetostatic simulation, the magnetic separation of microsphere-bacteria complexes was modeled in conjunction with the infection model. The pharmacokinetic profiles of infection can be seen in the three cases in Figures 5-7. The blood bacterial load decreases to 1 CFU/mL in approximately 44.17 h for the immunonormal case, with the rest of the compartments taking longer to clear the bacteria; in fact, the liver does not reach the threshold within the simulated 96 hours (Figure 5). Nevertheless, based on the trend of decreasing bacterial concentrations, the liver should be able to clear the remaining bacteria in a reasonable amount of time. In the immunocompromised case, bacterial concentrations in all compartments continue increasing to lethal limits of 10¹⁰ CFU/mL (Figure 6). Upon administration of effective antibiotics, the kinetics curves follow a similar trajectory to the immunonormal case (Figure 7). The blood and spleen compartments take on an additional bacterial burden relative to the immunonormal case, suggesting that additional care should be taken to ensure minimal toxicity in these compartments.

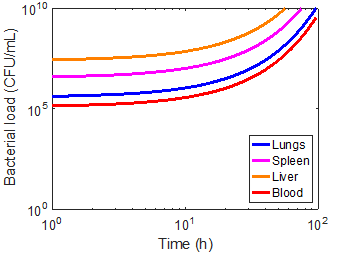
As a first approximation, a bead radius of 75 nm and a flow rate of 0.1 mL/min was used in the simulation. Applying the device to each of the immune cases did manage to capture a significant number of bacteria, but had virtually no impact on the overall infection kinetics (Figures 8-10). In the first ten hours of the immunocompromised scenario, the bacteria load of the device increased at a greater rate than in any of the other compartments. As the extracorporeal treatment progressed, bacterial loads in the body began to increase at a similar rate as in the device (Figure 10).

The amount of bacteria captured in the device is heavily dependent on the bacterial load of the blood compartment, as can be seen by comparing the immunonormal and antibiotic administration case. With a lower bacterial load in the immunonormal scenario, the device does not begin to capture bacteria until approximately the 2-hr mark (Figure 8), whereas the device shows significant capture within the first hour in the case of antibiotic administration (Figure 9). Thus, it may be prudent to reserve an efficacious extracorporeal separation for severe cases of bacteremia, where blood bacterial loads are higher, and omit the treatment for immunonormal treatments.

A grid search of the parameter space for bead radii from 25 nm to 500 nm and flow rates from 0.01-1.5 mL/min was employed to find any minimizers. No combination of bead radius and flow rate in this domain was found to significantly impact any of the infection metrics; standard deviations of any given metric across the space were more than two orders of magnitude less than the mean (Tables 3-5). Since the impact of the devices is so small, it is difficult to determine a meaningful minimizer with this method. Thus, any device with similar specifications would most likely not be able to treat a patient with bacteremia. An expanded search, especially with additional variables, could yield more meaningful minimizers. However, it must be noted that, due to the computational burden imposed by the differential equation solver, an efficient optimization algorithm must be used, such as the Nelder-Mead algorithm.

Table 3. Maximum bacterial load (CFU/mL) in the compartments across microsphere radius and flow rate parameter space. Mean ± standard deviation. N = normal, IC = immunocompromised, AB = antibiotic + IC.

	N	IC	AB
L	1.32 x 104 ± 6.82 x 10-10	1.02 x 1010 ± 5.36 x 107	2.48 x 104 ± 5.71 x 10-10
S	1.45 x 104 ± 4.02 x 10-10	9.61 x 1010 ± 5.04 x 107	2.41 x 105 ± 4.83 x 10-9
H	8.66 x 105 ± 5.47 x 10-9	6.76 x 1011 ± 3.48 x 109	1.66 x 104 ± 5.26 x 10-10
B	2.49 x 102 ± 2.63 x 10-2	3.39 x 109 ± 1.78 x 107	8.27 x 103 ± 1.55 x 10-10

Table 4. Time (h) to reach a threshold of 1 CFU/mL in the compartments across microsphere radius and flow rate parameter space. Mean ± standard deviation. N = normal, IC = immunocompromised, AB = antibiotic + IC.

	N	IC	AB
L	75.97 ± 0.001	N/A	60.76 ± 0.02
S	76.72 ± 0.002	N/A	74.41 ± 0.03
H	N/A	N/A	86.00 ± 0.03
B	44.17 ± 0.004	N/A	54.17 ± 0.02

Table 5. AUC (CFU/mL * h) in the compartments across microsphere radius and flow rate parameter space. Mean ± standard deviation. N = normal, IC = immunocompromised, AB = antibiotic + IC.

	N	IC	AB
L	1.06 x 105 ± 8.09 x 100	9.58 x 1010 ± 4.57 x 108	1.49 x 105 ± 6.44 x 101
S	1.16 x 105 ± 8.33 x 100	9.04 x 1011 ± 4.29 x 109	1.44 x 106 ± 5.87 x 102
H	6.93 x 106 ± 9.73 x 101	6.36 x 1012 ± 2.96 x 1010	9.94 x 106 ± 3.13 x 103
B	1.99 x 103 ± 1.57 x 10-1	3.19 x 1010 ± 1.52 x 108	4.96 x 104 ± 2.15 x 101

By examining the equations used in the magnetic separation and infection models, some insights can be gained as to why magnetic separation may not be wholly feasible as a treatment mechanism. In the binding efficiency equation,  has a major impact. Physiologically speaking,  is related to the density of particles in the fluid; that is to say, the blood cells that are already present interfere with the binding of the magnetic beads to the bacterial cells. Therefore, as  decreases, the overall binding efficiency, , goes to zero. If the major blood components were to be removed before magnetophoretic separation, the constant  would increase. However, this somewhat defeats the purpose of a magnetophoretic separation system.

With the magnetophoretic separation efficiency, both the bead radius, , and the bacterial radius, , have profound influence. Reducing the equation for the magnetophoretic force, , shows that the force depends linearly on the bead radius, but quadratically on the bacterial radius. This dependence arises from the fact that the available surface area of a bacterium increases with the square of the radius. This dependence on bacterial radius carries over to the magnetic separation efficiency, , but is less straightforward due to the impact of the hydraulic radius term, . The strong influence of the bacterial radius, therefore, cannot be ignored when developing a magnetic separation system. Additionally, the model may also be limited by the assumption of a spherical cell, while bacteria have a variety of shapes that could allow for more binding surface area than is accounted for.

Mechanical and biomechanical constraints of the microfluidic device were not incorporated into this model, but may restrict separation efficiency further. Although a creeping flow ( would increase the magnetic separation efficiency, such a flow would reduce the rate of change of bacterial load in the device and render it ineffective in clearing bacteria. The flow rate of blood through an extracorporeal separator has upper limits. Pressure within the microfluidic device has to be below the corresponding yield stresses. Additionally, the flow rate through the device must correspond to physiological flow rates; for example, the flow rate used in kidney dialysis has been proposed.

4. Conclusion

Incorporating a physically-based magnetic separation efficiency model into a physiologically-based pharmacokinetic model allows for a better understanding of the efficacy of a magnetics-based extracorporeal separation device. Here, it is demonstrated that with conventional magnets and microfluidics, clinical outcomes would most likely not improve, since bacterial load metrics were not significantly changed by any change to the microsphere radius or device flow rate. High-throughput, high-capture devices will be essential for there to be any improvement in patient outcomes.

Acknowledgements

This work was supported by the U.S. Department of Defense under contract W81XWH-13-1-0397, Vanderbilt University School of Engineering, and the Vanderbilt University Undergraduate Summer Research Program (VUSRP).

References