Volume 2, Year 2014 - Pages 30-39
DOI: 10.11159/ijtan.2014.005
Numerical Investigations of Heat Transfer Performance of Nanofluids in a Flat Plate Solar Collector
E. Ekramian, S. Gh. Etemad, M. Haghshenasfard*
Department of Chemical Engineering, Isfahan University of Technology, 84156-83111, Isfahan, Iran
haghshenas@cc.iut.ac.ir
Abstract - In this study, numerical simulation was used for prediction of heat transfer coefficients and thermal efficiency of water and various nanofluids in a flat plate solar collector. Multi Wall Carbon Nano-Tube MWCNT/water, Al2O3/water, and CuO/water nanofluids with mass percents of 1, 2, and 3 wt% have been used as working fluids. Effects of temperature and mass flowrate on the thermal efficiency of pure water and nanofluids were studied, and the standard efficiency curves of collector under different operating conditions were compared to the experimental data. Good agreement between the numerical predictions and experimental data was observed. The results showed that the heat transfer coefficient and thermal efficiency of CuO/water nanofluid are greater than other working fluids.
Keywords: Flat plate solar collector, Nanofluid, computational fluid dynamics (CFD), Thermal efficiency, Numerical simulation.
© Copyright 2014 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2014-02-19
Date Accepted: 2014-10-01
Date Published: 2014-10-15
Nomenclature:
- a: Absorption coefficient (dimensionless)
- Ac: Collector absorption area (m2)
- B: Body force (N/m3)
- CP: Specific heat capacity (J/kg-K)
- d: Diameter (m)
- g: Gravitational acceleration (m/s2)
- GT: Total global solar radiation (W/m2)
- h: Enthalpy (J/Kg)
- h: Local heat transfer coefficient (W/m2k)
- I: Radiation intensity (W/m2)
- k: Thermal conductivity (W/m-K)
- L: Length (m)
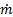 : Mass flow rate (kg/s)
: Mass flow rate (kg/s)- n: Refractive index (dimensionless)
- P: Pressure (Pa)
- Qu: Rate of energy gained (W)
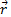 : Position vector (m)
: Position vector (m)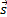 : Direction vector (m)
: Direction vector (m)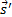 : Scattering direction vector (m)
: Scattering direction vector (m)- s: Path length (m)
- t: Time (s)
- T: Temperature (K)
- U: Interstitial velocity vector (m/s)
Greek letters
- φ: Volume fraction (dimensionless)
- τ: Tension tensor(N/m2)
- ρ: Density (kg/m3)
- µ: Viscosity (Pa.s)
- ε: Collector efficiency (dimensionless)
- ξ: Phase function (dimensionless)
- Ω: Solid angle (dimensionless)
- σs: Scattering coefficient (dimensionless)
- σ: Stefan-Boltzmann constant (5.669 * 10-8 W/m2-K4)
Subscript
- A: Ambient
- B: Balk
- bf: Base fluid
- i: Inlet
- nf: Nanofluid
- o: Outlet
- s: Solid particle
- w: Wall
1. Introduction
The use of solar energy has been increased in recent years due to the declining fossil fuel resources and environmental concerns about global warming and air pollution. Although solar power is expensive relative to conventional sources of energy like natural gas, but its overall cost continues to decrease with a quick rate [1-2]. One of the main applications of solar energy is solar water heating systems which sunlight is transferred to water or working fluid. The most common types of solar water heaters are evacuated tube collectors (44%), flat plate collectors (34%); and unglazed plastic collectors (22%) [3-4].
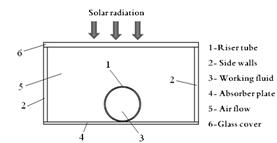
Flat plate solar collectors are the most common type of solar collectors for solar water-heating systems and are the simplest devices in this category. In a flat plate collector, the solar radiation energy is absorbed by a flat conductive plate and is transferred to the working fluid inside the tubes, which are attached on the absorber plate [5-7].
Many experimental and numerical studies were performed to investigate on the flat plat solar collectors [5-18], but heat transfer of nanofluids in the flat plate solar collectors is limited to a few published studies [19-23].
Recently an updated review of dynamic thermal models and CFD analysis of flat plate thermal solar collectors was presented by Tagliafico et al. [8]. Lumped-capacitance model and discretized model, which respectively were introduced by Close [9] and Klein et al. [10], have been analyzed in this work. The main investigations involving artificial neural network approach and CFD analysis on thermal solar collectors were also described.
Manjunath et al. [11] developed a CFD model to study the effect of surface geometry of solar collector on the thermal performance. The results of this configuration were compared to a dimple absorber plate. The CFD prediction showed that the average temperature of absorber plate and outlet water temperature for dimple configuration are higher than temperatures in flat plate solar collector.
Subiantoro and Tiow [12] proposed the analytical models for optimization of single and double glazing flat plate solar collectors. The models were used to predict the heat loss from the top cover of flat plate and the effect of the air gap spacing on the top heat loss.
Numerical simulations were adopted by Mintsa Do Ango et al. [13] for optimizing the design of polymeric flat plate solar collectors. Effects of operating conditions and geometrical parameters on thermal behavior of polymeric flat plate collector were studied. It was observed that the length of collector does not influence the collector performance and the efficiency of collector increases by increasing the air gap thickness up to 10 mm and then decreases slowly.
Numerical simulation was developed by Basavanna and Shashishekar [14] to study the thermal performance of triangular tube configuration on a flat plate solar collector. The special configuration of tubes makes larger contact area between the tube and the plate, which causes more energy to be absorbed. The numerical analysis have also been used by another researchers such as Karanth et al. [15], Selmi et al. [16], Turgut and Onur [17], and Fan et al. [18], for prediction of thermal performance of flat plate solar collectors. In these studies, the CFD technique is presented as a powerful, reliable, and cost saving tool for design and optimization of the solar collectors.
Review of the above-mentioned literature shows that the conventional fluids, such as water, are normally used as working fluids inside the solar collectors. Due to the low thermal performances of conventional fluids, new types of working fluids called "nanofluids" are now developed for enhancement of heat transfer efficiency of thermal devices.
Faizal et al. [19] studied the effects of various nanofluids on the thermal efficiency, and size reduction of the flat plat solar collectors. They found that by using the nanofluid as working fluid the efficiency of the collector increases.
Said et al. [20] performed some experiments for investigation on the nanofluid heat transfer on the flat plate solar collectors. Al2O3/water nanofluid with various concentrations has been used in this work and the effect of density and viscosity of nanofluid on the pumping power of solar collector were studied experimentally.
In an interesting work, Yousefi et al. [21] performed an experimental study to investigate the role of MWCNT/water nanofluid as a working fluid in a flat plate solar collector. In their work, MWCNT/water nanofluid has been used and the effects of inlet temperature, mass flowrate, and nanofluid concentration on the thermal efficiency of collector were studied. The results showed that the efficiency increases by increasing the mass flowrate under the small values of reduced temperature differences. In another work, they were studied the effect of pH values of MWCNT/water nanofluid on the efficiency of the solar collector [22]. They found that the difference between the pH of nanofluid and pH of isoelectric is an effective parameter on the collector efficiency.
Yousefi et al. [23] have also adopted the same procedure to investigate the effect of Al2O3/water nanofluid in a flat plate collector. The effects of operating conditions on the thermal efficiency were investigated and the results showed that the nanofluids are more efficient in comparison with water.
As the review of previous researches shows, numerical simulation of nanofluids inside the flat plate solar collectors has not been reported so far. In the present work, a comprehensive numerical study on solar flat plate collector including heat transfer, and solar radiation models were considered. Effects of temperature, nanofluid concentration, and fluid mass flow rate on the heat transfer coefficient and thermal efficiency of the solar collector were presented. The CFD predictions were compared to the experimental data reported by Yousefi et al. [21].
2. Numerical Simulation
For the numerical simulation of a solar collector, the radiation and convection heat transfer between the tube surfaces, sidewalls, and glass cover and the convective heat transfer in the circulating nanofluid inside the tube should be considered. In this work, the nanofluid is treated as a single-phase fluid. In the single-phase or homogeneous model, nanoparticles and base fluid are assumed to be in thermal and hydrodynamic equilibrium [24]. Newtonian laminar fluid flow is governed by the usual continuity, momentum and energy equations for three-dimensional simulations as follows:
-Continuity equation:
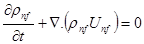
-Momentum equation:
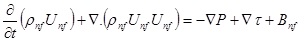
-Energy equation:
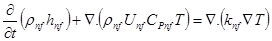
Radiation plays a key role on the
heat transfer and to reflect its effect, a radiation model is required. Four
radiation models are available in ANSYS FLUENT software [25]: the Rosseland,
P-1, surface to surface (S2S), discrete transfer (DTRM), and Discrete Ordinates
(DO) radiation models. Discrete ordinates radiation model has been considered
in this work. This model uses the radiative transfer equation (RTE) for
simulation of solar energy [25]. Eq. 4 shows the RTE equation in the direction  :
:
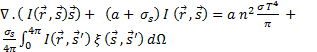
The physical properties of the nanofluids are calculated using the following correlations:
Pak and Choi's relation was used for calculation of the density [26]:
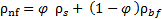
The viscosity of nanofluids is calculated from Drew and Passman [27] using the following relation:
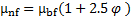
Zhou and Ni [28] suggested the following equation for calculation of the specific heat capacity of nanofluids. They showed this equation exhibits good agreement with the prediction from the thermal equilibrium model.
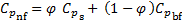
The effective thermal conductivity of nanofluids is calculated using a relation based on Maxwell's work [29]:
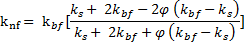
The governing equations were solved numerically using the finite volume technique, by a commercial CFD package, ANSYS-FLUENT 14. The SIMPLEC algorithm [30] was used to solve the pressure-velocity coupling in the momentum equations, backward differencing was used for the time and QUICK scheme was used for other terms discretization [31-32].
3. Geometry and Boundary Conditions
As mentioned earlier, the CFD predictions are compared to the experimental data reported by Yousefi et al. [21]. The experimental setup used in their work is shown in Figure 1 and consists of a closed circulation loop and a temperature-controlled tank for absorbing the heat load from the collector cycle. For transmit the heat load of the solar cycle to the working fluid, a heat exchanger inside the tank was used. The specification of this flat-plate solar collector is given in Table 1.

Table 1. The specifications of the flat-plate collector [21]
| Specification | Detail |
| External Dimension | 2000 x 1000 x 95 mm |
| Riser tubes material | Copper |
| Quantity | 9 tubes with 12.5 mm diameter |
| Absorber material | Aluminum |
| Absorber Absorptivity | 0.96 |
| Absorber Emissivity | 0.05 |
| Cover material | Low iron glass |
| Cover thickness | 4 mm |
| Cover Transmissivity | 0.92 |
| Gap spacing between absorber and cover | Air with 25 mm thick |
| Title angle of plate | 45° |
Computational domain of the flat plate solar collector is shown in Figure 2. Following assumptions are made in the simulation:
- Working fluid is considered as a continuous medium, Newtonian, and incompressible fluid
- The flow regime is considered to be laminar
- The flow field is symmetric with respect to y-z plane, therefor just one riser tube and absorber plate was considered for simulation
- Mass flowrates thorough all riser tubes are equal
In this paper, mesh generation for the computational domain was made in Gambit 2.2.30. The sensitivity of the simulation results were checked by comparing the results for 50000, 85000, 150000, 200000, and 450000 elements. The simulation results for the temperature difference between inlet and outlet fluid were similar for 150000 and 200000 elements, therefor, 150000 tetrahedral elements were considered.
In the simulation, the following boundary conditions were specified:
1- "Velocity inlet" boundary condition was used for the inlet zone. At this boundary, the velocity component, and temperature must be specified.
2- "Outflow" boundary condition was specified for the outlet zone.
3- "Symmetry" boundary condition was considered for the middle wall of the riser tube
4-"No-slip" boundary conditions were applied to the walls. The radiation parameters were specified for each zone. "Semi-transparent" option was enabled for upper wall to transmit the solar radiation into the collector area and the "opaque" option was used for the other surfaces.
Thermo-physical properties of the materials are shown in Table 2.
Table 2. Properties of material used in the simulation
| Material | Density (kg/m3) | Thermal conductivity (W/m.K) | Specific heat (J/kg.K) |
| Air | 1.225 | 0.0242 | 1006.43 |
| Water | 998.2 | 0.6 | 4182 |
| Copper | 8978 | 387.6 | 381 |
| Aluminum | 2719 | 202.4 | 871 |
| Glass | 2230 | 1.14 | 750 |
| CuO nanoparticles | 6000 | 33 | 551 |
| MWCNT | 1750 | 3000 | 710 |
| Al2O3 nanoparticles | 3890 | 35 | 880 |
4. Results and Discussion
Typical plots of temperature distribution and velocity vectors in the studied solar collector are shown in Figure 3.
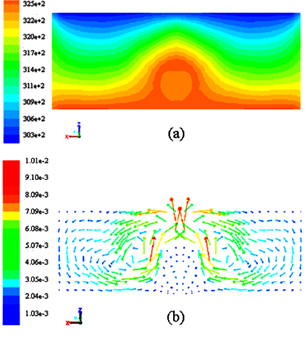
The velocity vectors show that the natural convection has an important role in heat transfer in the collector space. The color map, ranges from 303K to 329K for the temperature distribution between the absorber plate and glass cover. A criterion for a flat plate solar collector performance is the collector efficiency, which defined as the ratio of the heat gained by the working fluid to the total solar radiation incident on the collector surfaces. The relations are as follow:
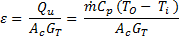
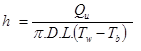
Numerical simulation is carried out to obtain the temperature distribution and thermal efficiency of various working fluids in a flat plate solar collector.
Figure 4 shows the experimental and predicted thermal efficiency versus reduced temperature parameter (Ti - Ta)/G for MWCNT/water nanofluid.

The experiments were carried out by MWCNT/water nanofluid with 0.2 wt% of mass fraction and 0.05 kg/s of mass flow rate. This figure is used for the validation of the present numerical results. The CFD simulations show a good agreement with the experimental data, emphasizing the accuracy of the numerical results. The average relative error between the experimental data and CFD predictions is about 8.5%.
Numerical thermal performances of MWCNT/water nanofluids with mass percent of 1, 2, and 3% in the solar collector are presented in Figs. 5& 6.
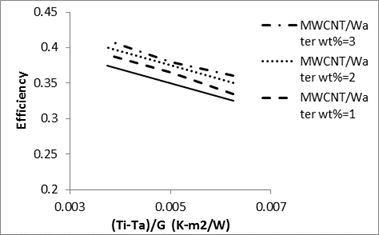
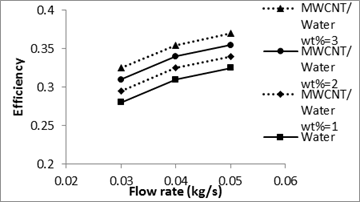
It can be seen that the heat transfer performance and thermal efficiency of MWCNT/water nanofluid are higher than those of the base-fluid. Based on the results of Figure 5, thermal efficiency increases with increasing the particle mass percent. Using of MWCNT/water nanofluid with 3% of mass fraction gives noticeable higher thermal efficiency than those of water by about 13.8%. Figure 6 shows that the thermal efficiency increases with increasing the mass flow rates. By increasing the mass flowrate from 0.03 to 0.05 kg/s, thermal efficiency of 1% MWCNT/water nanofluid increases by 13.2%.
According to Figure 6, by increasing the mass flowrate, the outlet temperature of working fluid and the absorber temperature decrease, therefore, the thermal efficiency increases. The same trends have been reported by Mintsa Do Ango et al. [13] and Cristofari et al. [33].
Figs. 7-8 show the thermal performance of Al2O3/water nanofluid in the solar collector.

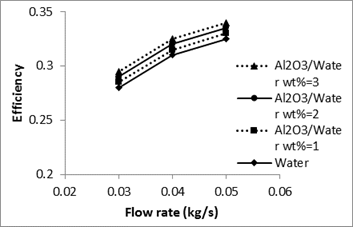
Similar to the MWCNT/water nanofluid, Al2O3/water nanofluid has more thermal efficiency in comparison with distilled water. For example, for a given reduced temperature parameter of 0.00625 (K.m2/W), the thermal efficiency of 3% nanofluid is about 6% and 9% higher than those of 1% nanofluid and pure water, respectively. Although the heat transfer coefficients of Alumina nanofluid are higher than MWCNT nanofluid, but the thermal efficiency of Alumina nanofluid is lower. This is probably due to the lower specific heat of MWCNT nanofluid in comparison with Alumina nanofluid.
Thermal performance of CuO /water nanofluid is shown in Figs. 9-10.
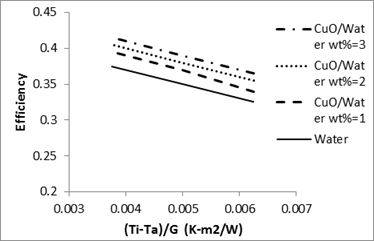
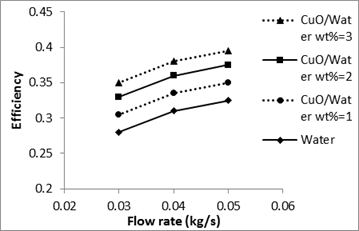
The results clearly show that by increasing the mass flowrate, the heat transfer performance increases, which is mostly due to the large energy exchange from the chaotic movement of nanoparticles [34]. At the constant mass flowrate of 0.03kg/s, thermal efficiency of 3% CuO/water nanofluid is about 20% and 13% higher than those of 1% nanofluid and distilled water, respectively.
In comparison with Al2O3/water nanofluid, the viscosity of CuO/water nanofluid is lower. The viscosity of nanofluids increases with increasing the nanofluid concentration, and this enhancement is greater for Al2O3/water nanofluid [35]. When the viscosity of nanofluid increases, the viscous forces are strong enough to overcome the Brownian motion of nanoparticles. The momentum and thermal boundary layer thickness under these conditions increases, therefore, the heat transfer coefficient decreases.
Effect of reduced temperature parameter on the thermal efficiency is shown in Figure 10. Increasing the reduced temperature parameter is the result of an increase in inlet temperature of working fluid [13]. By increasing the inlet temperature, the temperature of both absorber and glass increase, but the temperature of absorber enhances faster than the glazing temperature. Therefore, thermal losses through the glass cover are enhanced and consequently thermal efficiency of collector decreases.
Comparison between the thermal performances of various nanofluids is presented in Figs. 11-14.
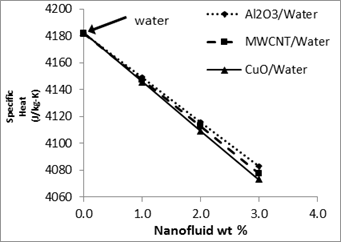
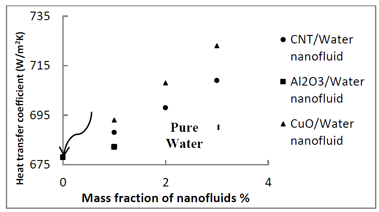
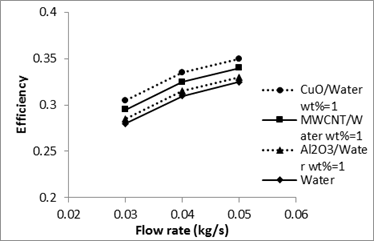
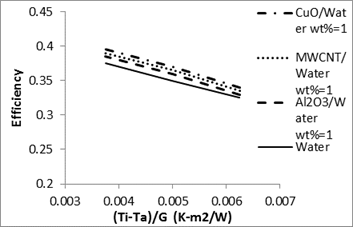
One of the most important parameters affecting on the thermal efficiency of the collector is specific heat of the working fluid. The specific heat for the nanofluids can be calculated by eq. 7. Figure 11 shows the specific heat of various nanofluids versus nanoparticle mass percent. It is clear that by increasing the mass percent, specific heat decreases. The low specific heat means that less energy needed to raise the temperature. CuO/water nanofluid possesses the lowest specific heat compared with other nanofluids. Therefore, we expect that the efficiency of the collector with CuO /water nanofluid be more than with other nanofluids. From Figs. 12-14 the heat transfer coefficient and thermal efficiency of CuO/water nanofluid are greater in comparison with other nanofluids. Figure 12 shows the heat transfer coefficients of various working fluids. It can be found that the heat transfer performances of all three nanofluids are higher than the pure water.
In general, heat transfer enhancement of nanofluids is due to the:
- Brownian motion of nanoparticles causes to turbulence effects and micro-convection, which enhance the heat transfer performance.
- High thermal conductivity of the nanofluids increases the heat transfer rate.
The average heat transfer coefficient of CuO /water nanofluid is about 4% and 2% higher than Al2O3/water and CNT/water nanofluids respectively. Enhancement of heat transfer coefficients of CuO /water, CNT/water and Al2O3/water nanofluids compared to the base fluid, are 6.5%, 4.5%, and 2% respectively. At the constant mass flowrate, thermal efficiency of CuO /water nanofluid with nanoparticle mass percent of 1% is about 3%, 6% and 9% higher than those of the CNT/water, Al2O3/water, and pure water, respectively.
5. Conclusions
The heat transfer performance of various nanofluids inside a flat plate solar collector was investigated numerically. MWCNT/water, Al2O3/water, and CuO/water nanofluids with mass percents of 1, 2, and 3 wt% have been used as working fluids. Effects of working fluid, mass flowrate, nanoparticle mass percent, and inlet temperature on the heat transfer coefficients and thermal efficiency were examined. The numerical predictions were validated using the experimental data in the literature with the same conditions and good agreement was obtained. The main conclusions are summarized as follow:
- Higher thermal conductivity of nanofluids and Brownian motion of nanoparticles cause better heat transfer performances. Heat transfer performance and thermal efficiency of employed nanofluids were higher than the base fluid.
- The Brownian motions and chaotic movement of nanoparticles enhances with increasing the nanofluid concentration. Therefore,, the thermal efficiency of the collector increases with increasing the nanoparticle mass percent. For example, the thermal efficiency of 3% CuO/water nanofluid is about 20% and 13% higher than those of 1% nanofluid and distilled water, respectively.
- By increasing the mass flowrate, the coolant outlet temperature, and the absorber temperature decrease. Increasing the flowrate improves the solar collector's thermal efficiency, but the coolant outlet temperature is then reduced. By increasing the mass flowrate from 0.03 to 0.05 kg/s, thermal efficiency of 1% MWCNT/water nanofluid increases by about 13.2%.
- By increasing the inlet temperature, the temperature difference between the absorber plate and glass cover decreases. Therefore, thermal losses is enhanced in collector, consequently thermal efficiency of collector reduces.
- The specific heat of nanofluids has a very important role on the thermal efficiency of the solar collectors. CuO/water nanofluid has lowest specific heat compared with Al2O3/water and CNT/water nanofluids. Therefore, based on the results the heat transfer coefficients and thermal efficiency of CuO/water nanofluid are greater than those of other nanofluids. The average heat transfer coefficient of CuO /water nanofluid is about 4% and 2% higher than those of Al2O3/water and CNT/water nanofluids respectively. For constant mass flowrate, thermal efficiency of 1% wt CuO /water nanofluid is about 3%, 6% and 9% higher than those for the CNT/water, Al2O3/water, and pure water, respectively.
Acknowledgements
The authors would like to express their appreciation to the Iranian Nanotechnology Initiative Council for providing financial support.
References
[1] M. AL-Khaffajy, R. Mossad, Optimization of the heat exchanger in a flat plate indirect heating integrated collector storage solar water heating system, Renew. Energ. 57 (2013) 413-421. View Article
[2] W. Kong, Zh. Wang, J. Fan, P. Bacher, B. Perers, Z. Chen, S. Furbo, An improved dynamic test method for solar collectors, Sol. Energ. 86 (2012) 1838-1848. View Article
[3] R. K. Naggi, Solar energy and its uses, First Edition, Mahaveer & sons, New Delhi, 2009. View Book
[4] N.K. Vejen, S. Furbo, L.J. Shah, Development of 12.5m2 solar collector panel for solar heating plants, Sol. Energ. Mat. Sol. C. 84 (2004) 205-223. View Article
[5] N. Akhtar, S.C. Mullick, Effect of absorption of solar radiation in glass-cover(s) on heat transfer coefficients in upward heat flow in single and double glazed flat-plate collectors, Int. J. Heat Mass Trans. 55 (2012) 125-132. View Article
[6] D. Dovic, M. Andrassy, Numerically assisted analysis of flat and corrugated plate solar collectors thermal performances, Sol. Energ. 86 (2012) 2416-2431. View Article
[7] A. Subiantoro, K. T. Ooi, Analytical models for the computation and optimization of single and double glazing flat plate solar collectors with normal and small air gap spacing, Appl. Energ. 104 (2013) 392-399. View Article
[8] L. A. Tagliafico, F. Scarpa, M. De Rosa, Dynamic thermal models and CFD analysis for flat-plate thermal solar collectors - A review, Renew. Sust. Energ. Rev. 30 (2014) 526-537. View Article
[9] D.A Close. Design approach for solar process, Sol. Energ. 11 (1967) 112-22. View Article
[10] S. Klein, J. Duffie, W. Beckman, Transient considerations of flat-plate solar collectors, J. Eng. Power - T ASME, 96A (1974) 109-13. View Article
[11] M.S. Manjunath, K.V. Karanth, N.Y. Sharma, A Comparative CFD study on Solar dimple plate collector with flat plate collector to augment the thermal performance, World Academy Sci. Eng. Tech. 70 (2012) 969-975. View Article
[12] A. Subiantoro, O.K. Tiow, Analytical models for the computation and optimization of single and double glazing flat plate solar collectors with normal and small air gap spacing, Appl. Energ. 104 (2013) 392-399. View Article
[13] A.C. Mintsa Do Ango, M. Medale, C. Abid, Optimization of the design of a polymer flat plate solar collector, Sol. Energ. 87 (2013) 64-75. View Article
[14] S. Basavanna, K. S. Shashishekar, CFD analysis of triangular absorber tube of a solar flat plate collector, Int. J. Mech. Eng. & Rob. Res. 2 (2013) 19-24. View Article
[15] K. Karanth, M. Manjunath, N. Sharma, Numerical simulation of a solar flat plate collector using discrete transfer radiation model (DTRM) - a CFD approach. In: Proceedings of the world congress on engineering. London(UK) (2011) 2355-2360. View Article
[16] M. Selmi, M. J. Al-Khawaja, A. Marafia, Validation of CFD simulation for flat plate solar energy collector, Renew. Energ. 33 (2008) 383-387. View Article
[17] O. Turgut, N. Onur, Three dimensional numerical and experimental study of forced convection heat transfer on solar collector surface. Int. Commun. Heat Mass Transf. 36 (2009) 274-279. View Article
[18] J. Fan, L. J. Shah, S. Furbo, Flow distribution in a solar collector panel with horizontally inclined absorber strips, Sol. Energ. 81 (2007) 1501-1511. View Article
[19] M. Faizal, R. Saidur, S. Mekhilef, M.A. Alim, Energy, economic and environmental analysis of metal oxides nanofluid for flat-plate solar collector, Energ. Convers. Manage. 76 (2013) 162-168. View Article
[20] Z. Said, M.H. Sajid, M.A. Alim, R. Saidur, N.A. Rahim, Experimental investigation of the thermophysical properties of AL2O3-nanofluid and its effect on a flat plate solar collector, Int. Commun. Heat Mass Transf. 48 (2013) 99-107. View Article
[21] T. Yousefi, E. Shojaeizadeh, F. Veysi, S. Zinadini, An experimental investigation on the effect of pH variation of MWCNT-H2O nanofluid on the efficiency of a flat-plate solar collector, Sol. Energ. 86 (2012) 771-779. View Article
[22] T. Yousefi, F. Veisy, E. Shojaeizadeh, S. Zinadini, An experimental investigation on the effect of MWCNT-H2O nanofluid on the efficiency of flat-plate solar collectors, Exp. Therm. Fluid Sci. 39 (2012), 207-212. View Article
[23] T. Yousefi, F. Veysi, E. Shojaeizadeh, S. Zinadini, An experimental investigation on the effect of Al2O3-H2O nanofluid on the efficiency of flat-plate solar collectors, Renew. Energ. 39 (2012) 293-298. View Article
[24]. M. Haghshenas Fard, M. Nasr Esfahany and M. R. Talaie, Numerical Study of Convective Heat Transfer of Nanofluids in a Circular Tube Two-Phase Model Versus Single-Phase Model, Int. Commun. Heat Mass Transf. 37 (2010) 91-97. View Article
[25] Fluent Inc, 2011. Fluent Release 14.0, USA.
[26] B.C. Pak, Y.I. Choi, Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles, Exp. Heat Transfer 8(1998)151-170. View Article
[27] D. A. Drew, S. L. Passman, Theory of multicomponent fluids, Springer, Berlin, (1999). View Book
[28] S.Q. Zhou, R. Ni, Measurement of the specific heat capacity of water-based Al2O3 Nanofluid, Appl. Phys. Lett. 92 (2008) 1-3. View Article
[29]. W. Yu, U. S. Choi, The role of international layers in the enhanced thermal conductivity of nanofluids: A renovated Maxwell model, J. Nanopart. Res. 5(2003) 167-171. View Article
[30] J. P. Van Doormal, G. D. Raithby, Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transfer 7 (1984) 147-163. View Article
[31]. S. V. Patankar, Numerical heat transfer and fluid flow, Hemisphere Publishing Corporation, Taylor and Francis Group, New York, (1980). View Book
[32]. H. Versteeg and M. Malasekera, An introduction to Computational Fluid Dynamics, McGraw Hill, New York, (1960). View Book
[33] C. Cristofari, G. Notton, P. Poggi, A. Louche, Modeling and performance of a copolymer solar water heating collector. Sol. Energ. 72 (2002) 99-112. View Article
[34]. W. Daungthongsuk, S. Wongwises, Comparison of the effects of measured and Computed thermo-physical properties of nanofluids on heat transfer performance, Exper. Therm. Fluid Sci. 34 (2010) 616-624. View Article
[35] J. Lee, P. E. Gharagozloo, B. Kolade, J. K. Eaton, K. E. Goodson, Nanofluid convection in microtubes, J. Heat Trans-T ASME, 132 (2010) 092401, 1-5. View Article

