International Journal of Theoretical and Applied Nanotechnology (IJTAN)

ISSN: 1929-1248

1. Introduction

Since their discovery CNTs (Iijima, 1991) attracted many scientists and engineers. Advantageous mechanical and physical properties like modulus of elasticity, tunability of band gap and piezoresistive gauge factor make them favourable to be adopted in several applications or to create even novel ones.

Promising applications of CNTs are their usage as reinforcing material (Bakshi et al., 2010), material for (anisotropic conductive) vertical interconnection in 3D packaging (Hermann et al., 2008), nano actuators (Senga et al., 2012), gas sensors (Leghrib et al., 2011) and acceleration sensors (Kang et al., 2009). As different the objectives of all those applications are, all have in common that CNTs are somehow connected to a different material. This connection influences the functionality and reliability of the system.

Several theoretical and experimental investigations have been conducted to access information about interface properties of CNTs and the connecting material. For example the study of wetting properties of CNTs to metals with first principle calculations by Maiti and Ricca (2004), giving insight to metal configuration dependent bonding behaviours between CNTs and metal surfaces. Nemec et al. (2006) conducted ab initio studies on CNT-metal interfaces and suggest a theoretical explanation of the good electronic CNT-Pd contact through weak hybridization of atom orbitals. Smolyanitski and Tewary (2011) investigated the lattice strain on a CNT-metal interface by molecular statics simulations, showing not only the influence of chirality on the strain, but suggesting also a local modification of the band gap. Tsuda et al. (2011) carried out experimental determination of interfacial shear strength of multi-walled CNT/PEEK composite in SEM equipped with an AFM-tip and found a close agreement of their determined value of 3.5-14 MPa with values estimated from macroscopic stress-strain behaviour. An experimental and numerical study of bonding behaviour of CNTs onto microelectrodes has been performed by Chen et al. (2011), explaining bonding technology by localized induction heating. Atomistic simulations of a CNT which is embedded in an organic matrix have been performed by Chandra et al. (2004) and in a next step these results have been used to feed a continuum cohesive zone model and showed the effand additionally been exposed to a pull-out loadingect of interface strength on the modulus of elasticity of the composite. Xia and Curtin (2004) investigated friction inside of multi walled CNTs with the result that pull-out forces depend strongly on defects in CNTs.

To our knowledge there are no further studies on the pull-out behaviour of CNTs embedded in a metal matrix, which would be required especially for reliability estimations of acceleration sensors (Hierold et al., 2007). Here CNTs are connected to metal microelectrodes: in application scenarios the acting forces on the CNT are considered to be crucial for the mechanical stability of the CNT-metal interface and thus for the electrical reliability of the sensor device. In this work we present our results on atomistic simulations of a pull-out test of a SWCNT embedded in a single crystal gold matrix by means of molecular dynamics. In section 2 we describe in detail our simulation models. Our results are presented and discussed in section 3. We give insight to our conclusions in section 4.

2. Simulation Setups

Molecular dynamics (MD) method (Gibson et al., 1960 and Abraham, 1986) is used to simulate the objective force-displacement relations. To this purpose we used the LAMMPS code (Plimpton, 1995) with velocity verlet algorithm. We consider two simulation setups. All CNTs regarded in this work are SWCNTs, so we use only CNT from now on. At first we have simulated the uniaxial tensile strain test on a single CNT. In the second setup we have simulated the pull-out test of a single CNT out of a gold single crystal.

2. 1. Uniaxial Tensile Strain Test

The geometry of our first simulation setup simply consists of a single CNT. The initial atomic positions are software generated (Veiga and Tomanek, 2007). The interaction of carbon atoms was modelled by the Adaptive Intermolecular Reactive Empirical Bond Order Potential of Stuart (2000). To save computational time we neglected the long range Lennard Jones and additional torsional contributions. This formulation is in effect very similar to the Reactive Empirical Bond Order Potential of Brenner et al. (2002). After building the CNT, it was structure optimized in a simulation box without periodic boundary conditions by using the conjugate gradient algorithm. After this we fixed the first ring of carbon atoms at one side of the CNT to their current positions and imposed random velocities corresponding to a temperature of 1 K to the remaining atoms. This was followed by a constant particle N, volume V and energy E (NVE-ensemble) calculation of positions, forces and velocities of the unfixed atoms. For all calculations with NVE integration the system temperature was controlled using a Berendsen thermostat (Berendsen et al., 1984). At a time step of 1 fs (this timestep is the case for all following described simulation setups) the system was equilibrated for 10 ps. During the last 1000 steps of this procedure the initial length of the CNT was determined by averaging the z-position of the outmost atom over time. To apply strain on the CNT in its axial direction the positions of the atoms on the free end of the CNT were updated by a discrete displacement step (0.4 Å) and kept fixed on these positions. This system was again equilibrated for duration of 10 ps. To get a measure for the force to keep the CNT in this strained state the z-components of all atom force vectors have been summed during the last 1000 steps of the equilibration and averaged. The force data has been saved in reference to the displacement. To complete the tensile test until failure of the CNT successive displacement steps have been carried out. As a result a displacement controlled tensile test in a quasi-static way has thus been simulated.

Simulation procedures of tensile tests with temperatures at 100 K, 200 K and 300 K were modified, because we observed in preliminary calculations that free standing CNTs begin to oscillate very heavily when they are heated up. In a subsequent tensile test then one would stretch a CNT which is not aligned to the pull direction, thereby bending the CNT. To avoid this, we equilibrated the system with periodic boundary conditions in length direction and measured the initial length by averaging as stated above. Then we enlarged the simulation box to skip the periodic boundary, constrained one end of the CNT and imposed the same displacement procedure as mentioned before. As a result, a well-defined uniaxial tensile strain test was conducted without bending the CNTs. Table 1 shows the design of experiment for the uniaxial tensile strain test.

2. 2. Pull-out Test

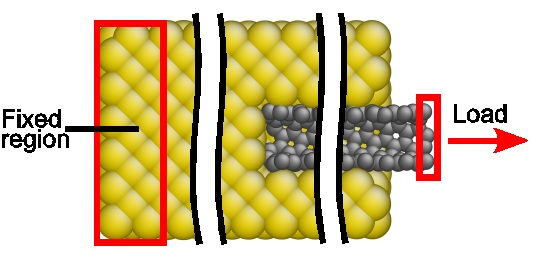
The geometry of the second simulation setup to simulate the force-displacement data during a pull-out test is shown in figure 1. It has been assembled in several steps.

First the initial CNT structure and gold metal block were placed into the simulation box. Periodic boundary conditions were applied in all directions. However, only perpendicular to the axis of the nanotube and lateral to the gold surface the periodic boundary conditions were effective, because in the z-direction a sufficiently large vacuum slab was modelled such that a metal surface was represented. To model the

Table 1. Design of experiment for uniaxial tensile strain test. Values for calculated modulus of elasticity are given

Nr.	Chirality	Temperature [K]	E [GPa]
1	(5,4)	1	911.25
2	(5,5)	1	918.03
3	(8,0)	1	1008.00
4	(6,3)	1	945.95
5	(6,3)	100	954.20
6	(6,3)	200	982.10
7	(6,3)	300	1014.00

interaction between gold atoms the EAM-potential type (Foiles et al., 1986) was utilised. The carbon gold interaction was modelled using a Lennard Jones potential with parameters from Huang et al. (2003) (σ = 2,985 Å, ε = 0.033 eV).

To achieve an initially relaxed structure subsequent conjugate gradient optimizations have been performed on the nanotube and the metal slab without influencing each other. This followed a removal of gold atoms in a cylindrical geometry with a defined depth of 50 Å and radius of 5 Å (this ideal hole diameter was determined in preliminary optimization studies) at the surface of the gold slab in [100] direction. In effect this means that the distance between two gold atoms on a minimum diameter measures ~ 11.6 Å. Diameters of all considered CNTs are ~ 6.3 Å. So the approximate distance between a carbon atom sited on the mean radius of the CNT and a gold atom sited on the minimum hole diameter is ~ 2.7 Å. This falls below the equilibrium distance of ~ 3.35 Å given in the used Lennard Jones parameterization; this fulfils our expectations, because the more atoms are attracting each other the larger the decrease in the distance of minimum energy.

After moving the CNT into the hole the structure was finally geometry optimized. Then the system was heated up to the desired temperature for 50 ps in a NPT integration assuming zero pressure and equilibrated by a subsequent NVE integration for 50 ps. During the last 10 ps the initial length of the free suspended CNT end has been averaged. Before dynamic runs have started the first four gold layers at the bottom of the gold slab have been restricted to their current positions. To carry out the pull-out test discrete

Table 2. Design of experiment for pull-out test. Values for calculated maximum pull-out forces are given

Nr.	Chirality	Temperature [K]	Fmax [eV/Å]
8	(5,4)	1	2.37
9	(5,5)	1	2.14
10	(8,0)	1	3.18
11	(6,3)	1	2.14
12	(6,3)	100	2.09
13	(6,3)	200	2.03
14	(6,3)	300	1.97

displacement steps (0.2 Å) and force calculations have been imposed in the same way as for the single CNT. The pull-out test models comprised, dependent on CNT type and length about 5000 atoms. Table 2 shows the design of experiment.

3. Results and Discussion

3. 1. Uniaxial Tensile Strain Test

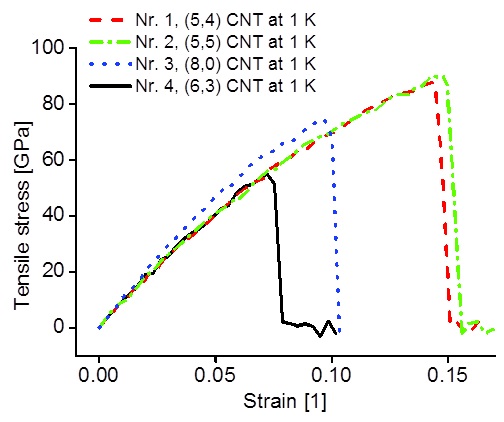
Figure 2 shows stress-strain data calculated from simulated force-displacement data of tensile strain tests on CNTs with different chirality at 1 K. For determination of the initial cross sectional area we calculated the mean radius of the CNT after structure optimization and used the van der Waals distance of graphite planes measuring 3.4 Å. In the region of small strains (~ 2.5%) slopes are very close. Assuming purely elastic behaviour, the modulus of elasticity can be related to the slope and calculated from Hooke`s law. Values are given in table 1. Good agreement with literature values of modulus of elasticity was found (Wu et al., 2008). Typical values are in a range of 1 ± 0.1 TPa.

Going to higher strains the deviation in stress-strain data between (8,0) CNT and the other ones increases and, as expected due to the asymmetric potential, the slope of all

stress-strain curves decreases with increasing strain. Large differences can be observed in the maximum strains and stresses. Though all CNTs have nearly the same length and radii both values differ by factor up to ~ 2. Fracture occurs exclusively at the fixed atoms of the CNTs due to fixing conditions.

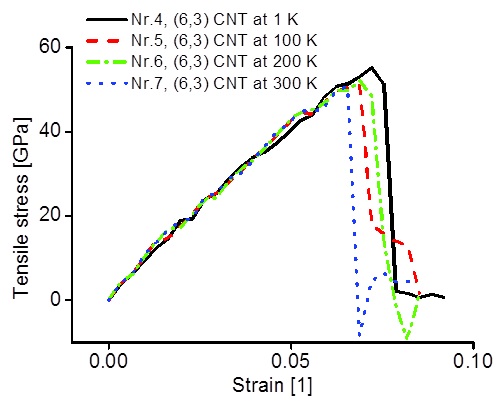
The curves in figure 3 display stress-strain curves of (6,3)-CNT at different temperatures. No distinctive influence of temperature on modulus of elasticity can be found. A slight negative trend of maximum stress with increasing temperature is observable.

3. 2. Pull-out Test

Figure 4 shows results of simulated force-displacement relations for pull-out tests of CNTs of different chirality at a temperature of 1 K. The difference between the results is obvious. The (6,3), (5,4) and (5,5) CNTs show a nearly linear regime until a maximum force has been reached, then the force is oscillating until the pull-out is completed and the force drops to zero. The first maximum in force can be attributed to the interaction of the terminal carbon atoms with gold atoms at the base of the hole. Slight differences can be seen in maximum pull-out forces (see table 2). When the separation between those atoms exceeds a threshold distance, then the force drops rapidly and begins to oscillate on a lower level. Furthermore the peaks remain nearly constant until the last three maxima, where a significant decrease is observed. The period of the force oscillation is approximately 4.1 Å which matches the [100] lattice vector of gold very well.

The zigzag type (8,0) CNT shows a different oscillation behavior. Following the first maximum the force oscillates in a period which corresponds to half of the [100] lattice vector of gold. The force maxima alternate between a lower and a

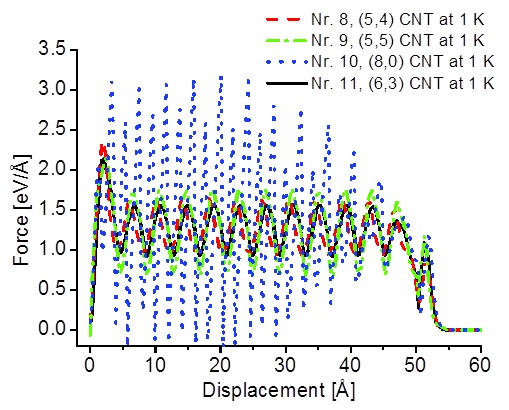
higher value, both of which are higher than the first. The global maximum force is reached at a pull-out displacement of ~ 23 Å. Compared to the overall initial increase of the maximum force the following decrease is much stronger. This behavior could be associated with number of carbon atoms which are in contact with gold atoms, but this is still not clarified and under investigation. Furthermore the force drops during the oscillations below zero, indicating that the CNT gets into compressive stress. However, although the oscillation amplitude of force is changing with increasing pull-out displacement, the mean force value is constant.

No fracture of the CNTs or within the gold solid could be observed. All CNTs slid out of the gold block, additionally no rearrangement of gold or carbon atoms occurred. Thus it can be stated that the separation occurred only between carbon and gold atoms due to the weak interaction between gold and carbon atoms modeled by the Lennard Jones potential.

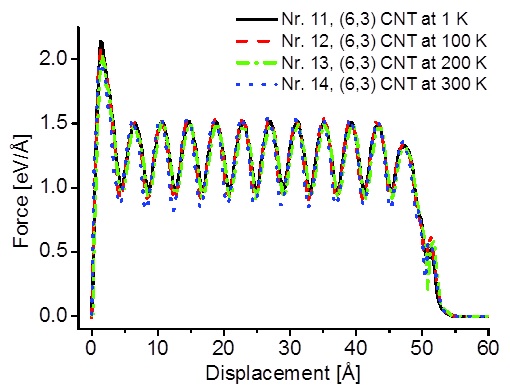
In figure 5 force-displacements curves of (6,3) CNTs for temperatures of 1 K, 100 K, 200 K and 300 K are depicted. In table 2 the maximum pull-out forces are given. While the temperature dependence of stiffness shows no clear trend a decrease of the first maximum force with increasing temperature can be observed. But this is only the case for the first maximum, the following maxima do not show this temperature dependence.

From a macroscopic point of view, the contact area independent behavior of the pull-out forces for (6,3), (5,4) and (5,5) CNTs when the first global maximum force is surmounted appears very unexpected. According to Amonton's Law with adhesion: F = µL + F₀ (Gao et al., 2004) the friction force F is a sum of an external normal force L times the coefficient of friction µ (load controlled contribution) and an internal force F₀ due to the adhesion between the two surfaces (adhesion controlled contribution).

Israelachvili (2011) states for molecularly smooth surfaces F₀ = σA, where A is the area of contact and σ the interfacial shear stress. It is difficult to clearly define an area of contact between molecularly smooth surfaces, but still this area of contact is proportional to the number of bonds. In our work the emphasis is on the adhesion controlled contribution, because we did not alter the normal pressure on the CNT-metal interface in our simulations. Considering then the relation between the friction force and the area of contact one would expect an overall decreasing force with increasing pull-out displacement aside the oscillation behavior. This is related to the fact that an increasing pull-out displacement leads to a decreasing number of interacting carbon and gold atoms. But this is only the case for the last three oscillations before the force drops to zero. Contributions to pull-out forces of radial bonding of gold and carbon atoms seem to be negligible. Our results are in very good qualitative agreement with Xia's and Curtin's (2004) analyses of the sliding behavior of an inner nanotube connected to an outer nanotube; both compose a multi walled CNT: the pull-out force remains constant with increasing pull-out displacement. Additionally our results follow the same trend (constant force with increasing pull-out displacement) of Li et al. (2011), who performed a molecular mechanics simulation of a pull-out of a CNT embedded in a polymer matrix. Thus the above given Amonton's Law with adhesion seems not to apply to our case without modifications.

But the different pull-out behavior of the (8,0) CNT implies a contribution of the atoms position between the CNT and the gold lattice to the friction force and the oscillation.

However, based on our results we state here that for the contact between a CNT and a single crystal gold matrix, after a threshold value of the embedding length has been exceeded, it has no effect on the required pull-out force, given that the

CNT is straight aligned and in <100> orientation with respect to the gold lattice. More investigations on this issue regarding interface structures have to be done.

3. 3. Comparison

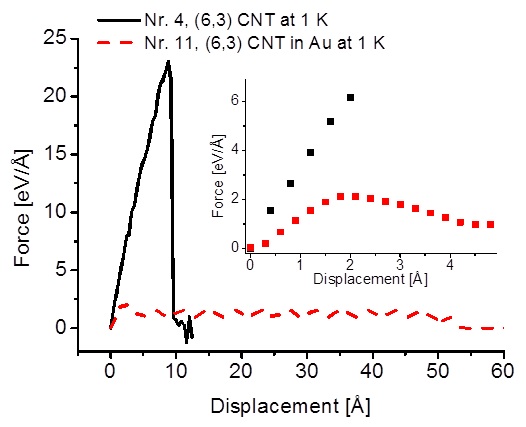
The results of force-displacement data of tensile strain test and a pull-out test for (6,3) CNT at 1 K are representatively shown in figure 6. It can be clearly seen that the stiffness of the initial loading region for the CNT-metal contact is much smaller compared to a CNT that is fixed at one end. The weakest bond is therefore stressed the most and in the case for the CNT-gold contact this is the interaction between gold and carbon. Therefore the quality of our investigated gold clamping is insufficient: At a maximum applied force on the CNT of ~ 2 eV/Å the CNT is strained to ~ 0.5 % and this is too small to act as a component in a piezo- resistive acceleration sensor to lead to a detectable signal in resistance change, for example. What is more, an increase of the embedding length seems to have no impact on this.

4. Conclusion

By means of molecular dynamics simulation we have performed uniaxial tensile strain tests on CNTs and pull-out tests on CNTs embedded in a single crystal gold lattice. We compared the resulting force-displacement data to do a theoretical estimation about clamping quality of the gold matrix and its dependencies. Main characteristic of our simulation procedure is an equilibration after each load step, this means that in sum all tests happened in a quasi-static way. We studied the influence of CNT chirality and the system temperature from 1 K to 300 K.

Our results indicate an influence of chirality on the pull-out behaviour and maximum pull-out forces. No significant impact of embedding length on pull-out forces could be concluded. The temperature effect is negligible except for maximum pull-out forces, where a slight negative trend could be found. However, statistics are needed to estimate temperature effects thoroughly.

Further investigations will concentrate on the influence of potential types and parameters to model the metal-carbon interaction, CNT-radius and more realistic cases of CNT-metal interface structures.

Acknowledgements

This work has been financed by the VW foundation within the project "Integration of dielectrophoretic deposited Carbon Nanotubes and their reliability in mechanical sensor systems" (I/85 086). All calculations have been performed on the Chemnitzer Hochleistungs-Linux-Cluster (CHiC).

References